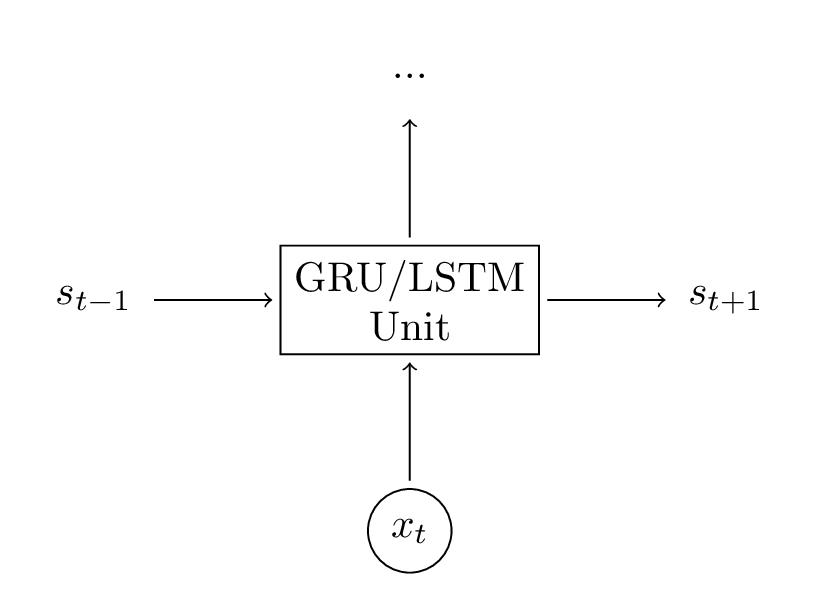
[RNN] Cài đặt GRU/LSTM
Bài giới thiệu RNN cuối cùng này được dịch lại từ trang blog WILDML.
Trong phần này ta sẽ tìm hiểu về LSTM (Long Short-Term Memory) và GRU (Gated Recurrent Units). LSTM lần đầu được giới thiệu vào năm 1997 bởi Sepp Hochreiter và Jürgen Schmidhuber. Nó giờ hiện diện trên hầu hết các mô hình có sử dụng học sâu cho NPL. Còn GRU mới được đề xuất vào năm 2014 là một phiên bản đơn giản hơn của LSTM nhưng vẫn giữ được các tính chất của LSTM.
Đây là bài cuối trong chuỗi bài giới thiệu về RNN:
- 1. Giới thiệu RNN
- 2. Cài đặt RNN với Python và Theano
- 3. Tìm hiểu về giải thuật BPTT và vấn đề mất mát đạo hàm
- 4. Cài đặt GRU/LSTM (bài này)
Mục lục
1. Mạng LSTM
LSTM được thiết kế nhằm tránh cho đạo hàm bị triệt tiêu như đã mô tả trong phần 3 của chuỗi bài viết. Về cơ bản, LSMT có kiến trúc như mạng RNN thuần nhưng khác nhau ở cách tính toán các trạng thái ẩn ($ \circ $ là kí hiệu của phép nhân poitwise - hay còn gọi là phép nhân Hadamard):
$$ \begin{aligned} i &= \sigma(x_t U^i + s_{t-1} W^i) \cr f &= \sigma(x_t U^f + s_{t-1} W^f) \cr o &= \sigma(x_t U^o + s_{t-1} W^o) \cr g &= \tanh(x_t U^g + s_{t-1} W^g) \cr c_t &= {c_{t-1} \circ f} + {g \circ i} \cr s_t &= \tanh(c_t) \circ o \end{aligned} $$
Những công thức trên nhìn khá phức tạp, nhưng chúng thực sự không khó. Với mạng RNN thuần, các trạng thái ẩn được tính toán dựa vào $ s_t = \tanh(U x_t + W s_{t-1}) $ với $ s_t $ là trạng thái ẩn mới, $ s_{t-1} $ là trạng thái ẩn phía trước và $ x_t $ là đầu vào của bước đó. Như vậy, đầu vào và đầu ra của LSTM cũng không khác gì so với RNN thuần, chúng chỉ khác cách tính toán mà thôi. Chính cách tính toán đặc biệt này giúp cho LSTM tránh được tình trạng đạo hàm bị triệt tiêu ở các bước phụ thuộc xa.
Chi tiết về cách LSTM tránh được chuyện đó bạn có thể đọc bài viết của anh Chirs Olah tại đây (bản dịch tại đây). Về cơ bản ta có thể tóm tắt LSTM như sau:
- $ i, f, o $ lần lượt được gọi là cổng vào, cổng quên và cổng ra. Từ công thức ở trên, ta có thể thấy giống hệt nhau và chỉ khác nhau ở tham số ma trận. Chúng được gọi là cổng bởi nó dùng để lọc thông tin đi qua đó. Với đặc điểm của hàm sigmoid nằm trong khoảng $ [0, 1] $ khi nhân với một véc-tơ thì ta có thể quyết định được có bao nhiêu thông tin được giữ lại. Ví dụ, với $ 0 $ thì phép nhân sẽ làm triệt tiêu véc-tơ tương đương với việc không có thông tin nào đi qua cổng được. Còn với $ 1 $ thì phép nhân không làm thay đổi véc-tơ đi qua, nên ta nói rằng toàn bộ thông tin qua nó được được bảo đảm. Cổng vào giúp ta chỉ định được bao nhiêu thông tin của đầu vào sẽ ảnh hưởng tới trạng thái mới. Cổng quên thì giúp ta bỏ đi bao nhiêu lượng thông tin ở trạng thái trước đó. Còn cổng ra sẽ điều chỉnh lượng thông tin trạng thái trong có thể ra ngoài và truyền tới các nút mạng tiếp theo. Ở đây, toàn bộ các cổng có cùng một kích cỡ và bằng số lượng trại thái ẩn của bạn: $ d_s $.
- $ g $ là trạng thái ẩn ứng cử được tính toán dựa trên đầu vào hiện tại và trạng thái trước. Công thức tính của nó không khác gì so với RNN thuần (ta chỉ đổi tên ở công thức trên: $ U = U_g $ và $ W = W_g $). Tuy nhiên, thay vì lấy giá trị đó làm trạng thái đầu ra như RNN thuần thì ta sẽ lọc thông tin của nó bằng cổng vào trước khi đưa nó làm trạng thái ẩn mới.
- $ c_t $ là bộ nhớ trong của LSTM. Nhìn vào công thức trên ta có thể thấy rằng nó là tổng của bộ nhớ trước đã được lọc bởi cổng quên và trạng thái ẩn ứng cử được lọc bởi cổng vào. Nói nôm na là nó là sự kết hợp của bộ nhớ trước và đầu vào hiện tại.
- Sau khi có được $ c_t $ rồi, ta sẽ đưa nó qua cổng ra để lọc thông tin một lần nữa để có được trạng thái mới $ s_t $.
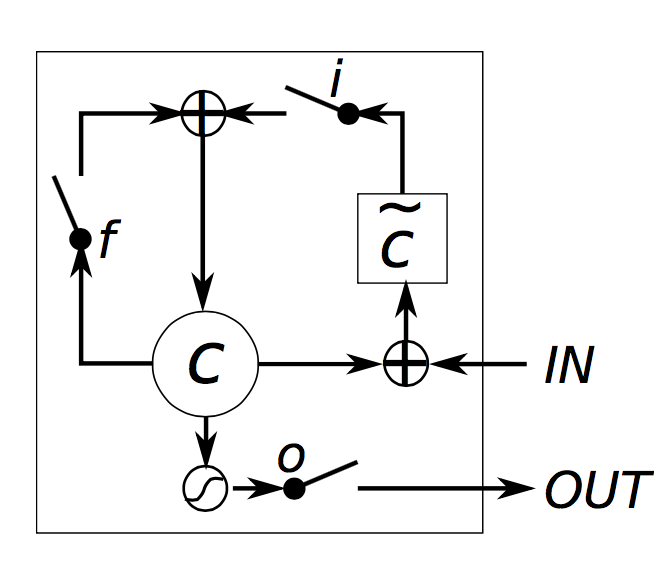 LSTM Gating. Chung, Junyoung, et al. “Empirical evaluation of gated recurrent neural networks on sequence modeling.” (2014)
LSTM Gating. Chung, Junyoung, et al. “Empirical evaluation of gated recurrent neural networks on sequence modeling.” (2014)RNN thuần có thể coi là một trường hợp đặc biệt của LSTM. Ở sơ đồ trên, nếu ta để giá trị đầu ra của cổng vào luôn là 1 và đầu ra của cổng quên luôn là 0 (không nhớ trạng thái trước), thì ta sẽ được mô hình RNN thuần. Cơ chế cổng của LSTM chính là chìa khóa giúp cho nó không bị mất mát đạo hàm, hay nói cách khác là có thể học được cả phụ thuộc xa.
Lưu ý rằng, mô hình LSTM ở trên chỉ là kiến trúc cơ bản của LSTM mà thôi. Trong thực tế có nhiều kiến trúc LSTM đã được xây dựng để giải quyết từng vấn đề cụ thể. Nếu bạn cần tìm hiểu sự khác nhau của chúng thì có thể đọc bài này của Odyssey. Một kiến trúc phổ biến của LSTM là sử dụng các kết nối peephole nhằm giúp các cổng có thể sử dụng được cả trạng thái trong $ c_{t-1} $ để đưa ra phán đoán hợp lý hơn.
2. Mạng GRU
Ý tưởng của GRU cũng khá giống với LSTM:
$$ \begin{aligned} z &= \sigma(x_t U^z + s_{t-1} W^z) \cr r &= \sigma(x_t U^r + s_{t-1} W^r) \cr h &= \tanh(x_t U^h + (s_{t-1} \circ r) W^h) \cr s_t &= {(1 - z) \circ h} + {z \circ s_{t-1}} \end{aligned} $$
GRU chỉ có 2 cổng: cổng thiết lập lại $ r $ và cổng cập nhập $ z $. Cổng thiết lập lại sẽ quyết định cách kết hợp giữa đầu vào hiện tại với bộ nhớ trước, còn cổng cập nhập sẽ chỉ định có bao nhiêu thông tin về bộ nhớ trước nên giữa lại. Như vậy RNN thuần cũng là một dạng đặc biệt của GRU, với đầu ra của cổng thiết lập lại là 1 và cổng cập nhập là 0. Cùng chung ý tưởng sử dụng cơ chế cổng điều chỉnh thông tin, nhưng chúng khác nhau ở mấy điểm sau:
- GRU có 2 cổng, còn LSTM có tới 3 cổng.
- GRU không có bộ nhớ trong $ c_t $ và không có cổng ra như LSTM.
- 2 cổng vào và cổng quên được kết hợp lại thành cổng cập nhập $ z $ và cổng thiết lập lại $ r $ sẽ được áp dụng trực tiếp cho trạng thái ẩn trước.
- GRU không sử dụng một hàm phi tuyến tính để tính đầu ra như LSTM.
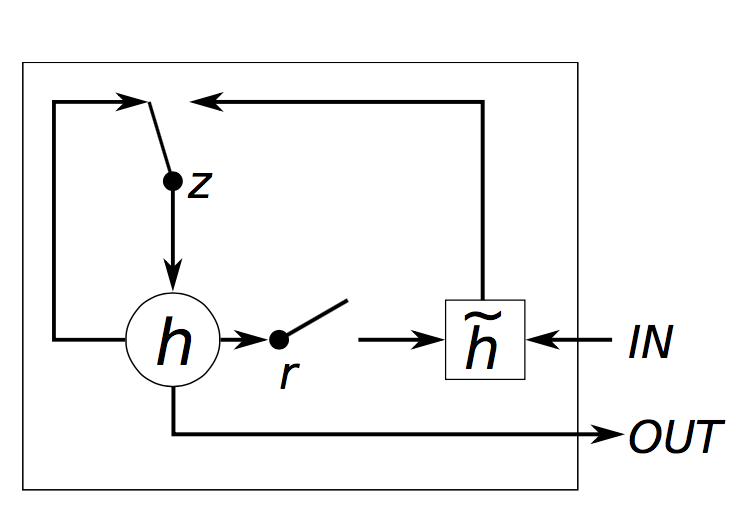 GRU Gating. Chung, Junyoung, et al. “Empirical evaluation of gated recurrent neural networks on sequence modeling.” (2014)
GRU Gating. Chung, Junyoung, et al. “Empirical evaluation of gated recurrent neural networks on sequence modeling.” (2014)3. GRU vs LSTM
Cả 2 kiến trúc này đều có thể giải quyết được vấn đề mất mát đạo hàm, nhưng cái nào ngon hơn cái nào? GRU còn khá trẻ tuổi (2014) so với ông chú LSTM của mình (1997) và tiềm năng của nó vẫn chưa được khám phá hết. Tuy nhiên thông qua một số đánh giá thì không cái nào thực sự là ăn được hẳn cái nào. Nhiều bài toán, việc điều chỉnh các siêu tham số (hyperparameters) như số tầng chẳng hạn lại có ý nghĩa hơn là việc chọn kiến trúc LSTM hay GRU. Nhưng cũng có những bài toán mà GRU được chọn bởi nó nhanh hơn hoặc cần ít dữ liệu hơn do GRU ít tham số hơn. Cũng có những lúc nếu bạn có đủ dữ liệu thì LSTM lại tỏ ra mạnh mẽ hơn và đạt được kết quả tốt hơn. Để tìm hiểu thêm về một số đánh giá so sánh giữa 2 mô hình này, bạn có thể tham khảo tại đây và cả đây nữa.
4. Cài đặt
Ta sẽ dựa vào đoạn mã bữa trước ta đã xây dựng với Theano để cài đặt LSTM/GRU. Lô-gic chương trình sẽ không thay đổi vì LSTM hay GRU chỉ đơn giản là thay đổi cách tính trạng thái ẩn mà thôi. Nên ta chỉ cần thay đổi đoạn mã tính toán đó dựa và các công thức phía trên là được. Đoạn mã bên dưới đây sẽ chỉ mô ta việc tính toán đó, còn toàn bộ mã nguồn đầy đủ các bạn có thể xem trên Github.
1 | |
Nhìn khá đơn giản phải không? Thế còn việc tính đạo hàm thì sao?
Cũng như phần trước ta có thể tính đạo hàm với E, W, U, b và c một cách tương tự bằng quy tắc chuỗi vi phân.
Tuy nhiên, ở đây tôi sử dụng luôn thư viện Theano để tính đạo hàm cho tiện.
1 | |
Giờ thì chương trình của ta đã khá đẹp rồi, nhưng để đạt được kết quả tốt thì cần một số mẹo nữa.
4.1. Cập nhập tham số với rmsprop
Giải thuật SGD (Stochastic Gradient Descent) thường sẽ không tìm được điểm tối ưu nếu độ học (learning rate) của ta lớn và sẽ rất chậm nếu độ học nhỏ.
Để giải quyết vấn đề đó, hàng loạt các biến thể khác nhau của SGD đã được ra đời như
Momentum Method,
AdaGrad,
AdaDelta,
rmsprop…
Để tìm hiểu thêm các giải thuật này khác nhau ra sao bạn có thể đọc bài so sánh này để có một cái nhìn tổng quan về chúng.
Trong phần này tôi chọn rmsprop để thực hiện việc tối ưu tham số.
Ý tưởng cơ bản của giải thuật này là thay đổi độ học theo từng tham số một dựa vào tổng các đạo hàm trước.
Một cách trừu tượng, ta có thể nói rằng đối với các thuộc tính thường xảy ra hơn thì sẽ có độ học nhỏ hơn do tổng đạo hàm của chúng lớn hơn, còn các thuộc tính ít xảy ra thì sẽ có độ học lớn hơn.
Việc cài đặt rmsprop khá đơn giản. Với mỗi tham số ta tạo một biến để lưu tạm tham số và sẽ cập nhập dần tham số và biến đó trong quá trình giảm đạo hàm như sau:
1 | |
decay thường là 0.9 hoặc 0.95, còn 1e-6 được cộng thêm vào để tránh việc chia cho 0 khi cacheW bằng 0.
4.2. Thêm một tầng nhúng
Sử dụng các từ nhúng như word2vec và GloVe
là một phương pháp phổ biến để cài thiện độ chính xác của mô hình.
Thay vì sử dụng các véc-tơ one-hot để biểu diễn các từ thì ta sử dụng các véc-tơ có kích cỡ nhỏ như word2vec hay GloVe có mang ngữ nghĩa sẽ mang lại hiệu năng tốt hơn.
Sử dụng các véc-tơ này tương đương với việc ta sử dụng các đầu vào đã được huấn luyện trước (pre-training), nên độ chính xác có thể được cải thiện.
Một cách trừu tượng, bạn cho mạng nơ-ron biết được các từ nào là tương tự nhau có thể giúp nó hiểu được ngôn ngữ hơn và việc học sẽ được cắt giảm bớt đi.
Sử dụng các véc-tơ được huấn luyện trước này còn có lợi khi bạn có ít dữ liệu vì nó cho phép mạng có thể sinh ra được nhiều từ mà bạn chưa có trong tập dữ liệu dựa vào các từ đồng nghĩa của véc-tơ.
Ở đây tôi không thêm tầng nhúng vào, nhưng việc thêm này cũng không khó vì chỉ đơn giản là thay thế ma trận E trong đoạn mã của ta là xong.
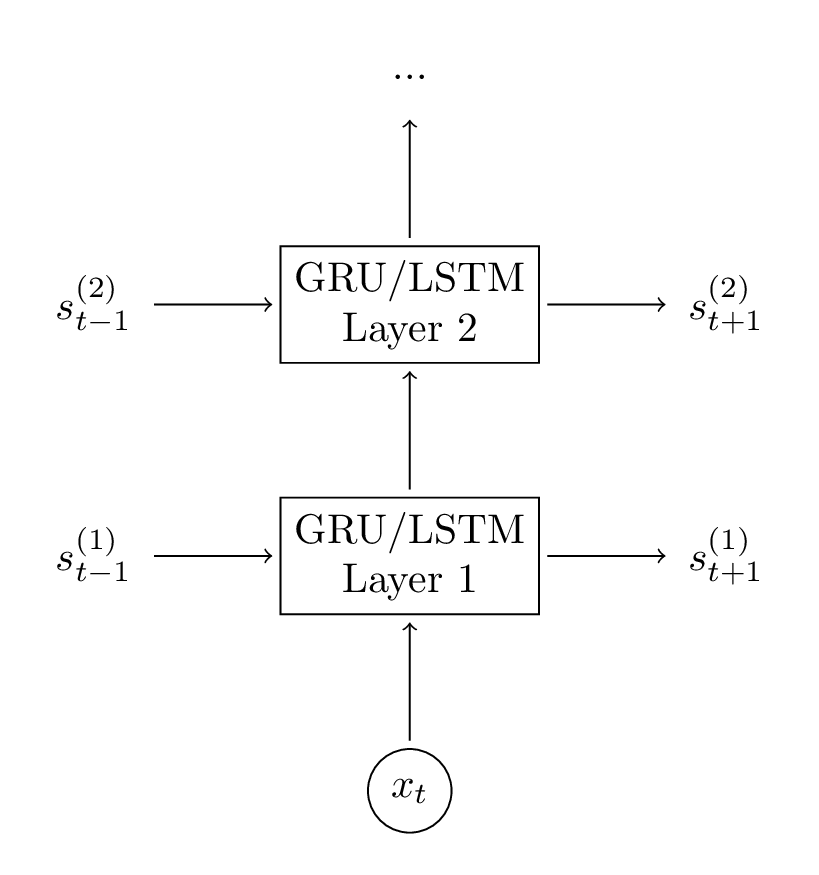
4.3. Thêm tầng GRU thứ 2
Thêm một tầng thứ 2 có thể giúp mô hình của ta tương tác được ở mức độ cao hơn. Bạn có thể thêm nhiều tầng hơn nữa, nhưng chắc chắn rằng đừng để mô hình của bạn bị khớp quá (overfitting) khi dữ liệu của bạn không đủ lớn. Ở đây tôi không có nhiều dữ liệu, nên tôi cũng chỉ muốn mô hình của mình trả ra kết quả ngay sau 2, 3 tầng mạng.
Việc tính toán ở các tầng là tương tự nhau, nên ta chỉ cần thêm đoạn mã tính cho tầng vừa thêm là được.
1 | |
Mã đầy đủ tôi có để trên Github, nếu hứng thú các bạn có thể tham khảo trên đó.
4.4. Hiệu năng
Đoạn mã tôi xây dựng ở đây chỉ dành cho mục đích học tập, không phải dành cho phát triển sản phẩm, bởi vậy hiệu năng thực sự là không tốt. Để hoàn thiện hơn thì ta cần nhiều mẹo khác để tối ưu hiệu năng của RNN, nhưng có lẽ quan trọng nhất là cập nhập cùng lúc nhiều tham số. Thay vì học từng câu một, ta có thể nhóm các câu có cùng độ dài với nhau (thậm chí có thể thêm các kí tự vào để được các câu có cùng độ dài), sau đó thực hiện phép nhân ma trận và cộng tổng đạo hàm lại cùng lúc. Vì thực hiện phép nhân một ma trận cỡ lớn có thể thực hiện rất hiệu quả với GPU, chứ không cần phải chia nhỏ ra để xử lý sẽ rất chậm.
Ngoài ra, bạn nên sử dụng các thư viện học sâu có sẵn để thực hiện. Do các thư viện này đã được tối ưu hóa để đạt được hiệu năng tốt rồi, nên bạn hoàn toàn có thể an tâm sử dụng và tập trung vào nghiệp vụ của chương trình. Nhiều mô hình nếu tự xây dựng có thể mất vài ngày tới vài tuần để huấn luyện, nhưng chỉ mất vài giờ huấn luyện nếu sử dụng các thư viện có sẵn. Như vậy thì dại gì mà ta lại đi xây dựng lại nữa. Tôi thì thích Keras hơn cả do nó khá dễ sử dụng và có nhiều ví dụ dễ hiểu cho RNN.
5. Kết quả
Tôi có luyện sẵn một mô hình với lượng từ vựng là 8000, chuỗi véc-tơ có kích cỡ là 48 và 128 tầng GRU. Cách sài nó tôi cũng đã viết đầy đủ để các bạn tiện sử dụng trên Github, các bạn có thể tải về và chạy xem sao nhé.
Dưới đây là một số kết quả mà tôi chọn lọc ra sau khi chạy chương trình:
- “I am a bot , and this action was performed automatically .”
- “I enforce myself ridiculously well enough to just youtube.”
- “I’ve got a good rhythm going !”
- “There is no problem here, but at least still wave !”
- “It depends on how plausible my judgement is .”
- ”( with the constitution which makes it impossible )”
Trông khá ngon vì ngữ nghĩa có vẻ ổn hơn lần trước. Điều đó chứng tỏ mạng của ta đã có thể xử lý được các phụ thuộc xa khá tốt rồi.
Tới đây tôi xin dừng vài giới thiệu về RNN của mình, hi vọng là bạn đã có một cái nhìn tổng qua về mô hình mạng hồi quy và có thể áp dụng nó để làm ra nhiều sản phẩm thú vị. Nếu bạn có thắc mắc hay góp ý gì thì đừng quên bình luận ở bên dưới nhé.