Bài giới thiệu RNN thứ 2 này được dịch lại từ trang blog WILDML.

Trong phần này chúng ta sẽ cài đặt một mạng nơ-ron hồi quy từ đầu sử dụng Python và tối ưu với Theano - một thư viện tính toán trên GPU. Tôi sẽ chỉ đề cập các thành phần quan trọng để giúp bạn có thể hiểu được RNN, còn toàn bộ mã nguồn bạn có thể xem trên Github.

Đây là bài thứ 2 trong chuỗi bài giới thiệu về RNN:

Mục lục

1. Mô hình hoá ngôn ngữ

Mục tiêu của ta là xây dựng một mô hình ngôn ngữ sử dụng RNN. Giả sử ta có một câu với $ m $ từ, thì một mô hình ngôn ngữ cho phép ta dự đoán được xác xuất của một câu (trong tập dữ liệu) là:

$$ P(w_1, …, w_m) = \prod_{i=1}^n(w_i | w_1, …, w_{i-1}) $$

Ở đây, xác xuất của câu chính là tích xác xuất của mỗi từ. Trong đó, xác xuất mỗi từ là xác xuất với điều kiện là biết trước các từ trước nó. Ví dụ, xác xuất của câu: “He went to buy some chocolate” sẽ là xác xuất của “chocolate” khi đã biết “He went to buy some”, nhân với xác xuất của “some” khi đã có “He went to buy”,…

Tại sao cách tính này lại hữu dụng? Tại sao ta lại cần phải tính xác xuất cho câu?

Thứ nhất, một mô hình như vậy có thể được sử dụng như một cơ chế đánh giá. Ví dụ, một hệ thống dịch máy thường sinh ra nhiều khả năng cho một câu đầu vào. Lúc này bạn có thể sử dụng mô hình ngôn ngữ để chọn ra khả năng có xác xuất cao nhất. Một cách trừu tượng, câu có xác xuất cao có thể là câu đúng ngữ pháp. Cách đánh giá này cũng tương tự như với hệ thống nhận giạng giọng nói.

Nhưng việc giải quyết bài toán mô hình hoá ngôn ngữ cũng có những điều rất tuyệt vời. Vì ta có thể dự đoán được xác xuất của một từ khi đã biết các từ trước đó, nên ta có thể làm được hệ thống tự động sinh văn bản. Mô hình như vậy được gọi là “mô hình sinh” (generative model). Ta lấy một vài từ của một cầu rồi chọn dần ra từng câu một từ xác xuất dự đoán được cho tới khi ta có một câu hoàn thiện. Cứ lặp lại như vậy ta sẽ có được một văn bản tự sinh. Về khả năng của ngôn ngữ, anh Andrej Karpathy có viết lại khá tuyệt vời trên blog anh ấy. Các mô hình của anh ấy được huấn luyện với các kí tự đơn thay vì cả một từ hoàn chỉnh và có thể sinh ra được rất nhiều thứ từ Shakespeare cho tới Linux Code.

Lưu ý rằng các công thức xác xuất ở trên của mỗi từ là xác xuất có điều kiện là biết trước tất cả các từ trước nó. Trong thực tế, bởi khả năng tính toán và bộ nhớ của máy tính có hạn, nên với nhiều mô hình ta khó có thể biểu diễn được những phụ thuộc xa (long-term dependences). Vì vậy mà ta chỉ xem được một vài từ trước đó thôi. Về mặt lý thuyết, RNN có thể xử lý được cả các phụ thuộc xa của các câu dài, nhưng trên thực tế nó lại khá phức tạp. Nguyên nhân là gì, thì ta sẽ cùng xem ở bài viết sau.

2. Dữ liệu và tiền xử lý

Để huấn luyện mô hình ngôn ngữ, ta cần dữ liệu là văn bản để làm dữ liệu huấn học. May mắn là ta không cần dán nhãn cho các mô hình ngôn ngữ mà chỉ cần tập văn bản thô là đủ. I đã tải 15,0000 bình luận trên Reddit từ cơ sở dữ liệu BigQuery của Google. Và hi vọng là các văn bản được sinh ra trông có vẻ như của người dùng Reddit. Cũng như hầu hết các dự án học máy khác, ta đầu tiên cần phải tiền xử lý dữ liệu thô cho đúng định dạng đầu vào.

2.1. Phân rã dữ liệu thô

Ta có dữ liệu văn bản thô, nhưng ta lại muốn dự đoán từng từ một, nên ta cần phải phân ra dữ liệu ta thành từng từ riêng biệt. Đầu tiên ta sẽ phân ra thành từng câu một, sau đó lại phân câu thành từng từ riêng biệt. Ta có thể chia các bình luận bằng dấu cách, nhưng cách đó không giúp ta phân tách được các dấu chấm câu. Ví dụ: “He left!” cần phải chia thành 3 phần: “He”, “left”, ”!”. Để đỡ phải vất vả, ta sẽ sử dụng NLTK với hàm word_tokenize và sent_tokenize để phân tách dữ liệu.

2.2. Bỏ các từ ít gặp

Trong hầu hết các văn bản có những từ chỉ xuất hiện 1 hoặc 2 lần, những từ không xuất hiện thường xuyên như thế này ta hoàn toàn có thể loại bỏ. Càng nhiều từ thì mô hình của ta học càng chậm (ta sẽ nói lý do sau), và chúng ta không có nhiều ví dụ sử dụng những từ đó nên không thể nào mà học cách sử dụng chúng sao cho chính xác được. Việc này cũng khá giống với cách con người học. Để hiểu cách sử dụng một từ chuẩn xác, bạn cần phải xem xét nó ở nhiều ngữ cảnh khác nhau.

Ta sẽ giới hạn lượng từ vựng phổ biến của ta bằng biến vocabulary_size (ở đây, tôi để là 8000, nhưng bạn cứ thay đổi nó thoải mái). Những từ ít gặp không nằm trong danh sách các từ phổ biến, ta sẽ thay thế nó bằng UNKNOWN_TOKEN. Ví dụ, nếu danh sách vựng của ta không có từ “nonlinearities” thì câu “nonlineraties are important in Neural Networks” sẽ được chuyển hoá thành “UNKNOWN_TOKEN are important in Neural Networks”. Ta sẽ coi UNKNOWN_TOKEN cũng là 1 phần của danh sách từ vựng và cũng sẽ dự đoán nó như các từ khác. Khi một từ mới được sinh ra, ta có thể thay thế UNKNOWN_TOKEN lại bằng cách lấy ngẫu nhiên một từ nào đó không nằm trong danh sách từ vựng của ta, hoặc ta có thể tạo ra một các từ cho tới khi từ được sinh ra nằm trong danh sách từ của ta.

2.3. Thêm kí tự đầu, cuối

Ta cũng muốn xem từ nào là từ bắt đầu và từ nào là từ kết thúc của một câu. Để làm được chuyện đó, ta cần phải thêm vào 2 kí tự đặc biệt cho mỗi câu là: SENTENCE_START liền trước câu và SENTENCE_END liền sau câu. Nó sẽ cho phép ta đặt câu hỏi là: Giờ ta có một từ là SENTENCE_START, thì từ tiếp theo của ta sẽ là gì? Từ tiếp theo chính là từ đầu tiên của câu.

2.4. Ma trận hoá dữ liệu

Đầu vào của RNN là các vec-tơ chứ không phải là các chuỗi. Nên ta cần chuyển đổi giữa các từ và địa chỉ tương ứng với index_to_word và word_to_index. Ví dụ, từ “friendly” ở vị trí 2001 trong danh sách từ vựng thì địa chỉ của nó sẽ là 2001. Như vậy tập dữ liệu $ x $ của sẽ có dạng: $ [0, 179, 314, 416] $, trong đó $ 0 $ tương ứng với SENTENCE_START. Còn các nhãn (dự đoán) $ y $ sẽ là $ [179, 341, 416, 1] $, trong đó $ 1 $ tương ứng với SENTENCE_END. Vì mục tiêu của ta là dự đoán các từ tiếp theo, nên $ y $ đơn giản là dịch một vị trí so với $ x $, và kết câu là SENTENCE_END. Nói cách khác, với dự đoán chuẩn xác cho từ $ 179 $ sẽ là $ 314 $.

train-theano.pytrain-theano.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
vocabulary_size = 8000
unknown_token = "UNKNOWN_TOKEN"
sentence_start_token = "SENTENCE_START"
sentence_end_token = "SENTENCE_END"

# Read the data and append SENTENCE_START and SENTENCE_END tokens
print "Reading CSV file..."
with open('data/reddit-comments-2015-08.csv', 'rb') as f:
    reader = csv.reader(f, skipinitialspace=True)
    reader.next()
    # Split full comments into sentences
    sentences = itertools.chain(*[nltk.sent_tokenize(x[0].decode('utf-8').lower()) for x in reader])
    # Append SENTENCE_START and SENTENCE_END
    sentences = ["%s %s %s" % (sentence_start_token, x, sentence_end_token) for x in sentences]
print "Parsed %d sentences." % (len(sentences))

# Tokenize the sentences into words
tokenized_sentences = [nltk.word_tokenize(sent) for sent in sentences]

# Count the word frequencies
word_freq = nltk.FreqDist(itertools.chain(*tokenized_sentences))
print "Found %d unique words tokens." % len(word_freq.items())

# Get the most common words and build index_to_word and word_to_index vectors
vocab = word_freq.most_common(vocabulary_size-1)
index_to_word = [x[0] for x in vocab]
index_to_word.append(unknown_token)
word_to_index = dict([(w,i) for i,w in enumerate(index_to_word)])

print "Using vocabulary size %d." % vocabulary_size
print "The least frequent word in our vocabulary is '%s' and appeared %d times." % (vocab[-1][0], vocab[-1][1])

# Replace all words not in our vocabulary with the unknown token
for i, sent in enumerate(tokenized_sentences):
    tokenized_sentences[i] = [w if w in word_to_index else unknown_token for w in sent]

print "\nExample sentence: '%s'" % sentences[0]
print "\nExample sentence after Pre-processing: '%s'" % tokenized_sentences[0]

# Create the training data
X_train = np.asarray([[word_to_index[w] for w in sent[:-1]] for sent in tokenized_sentences])
y_train = np.asarray([[word_to_index[w] for w in sent[1:]] for sent in tokenized_sentences])

Ví dụ, đây là một câu trong tập huấn luyện của ta:

x:
SENTENCE_START what are n't you understanding about this ? !
[0, 51, 27, 16, 10, 856, 53, 25, 34, 69]

y:
what are n't you understanding about this ? ! SENTENCE_END
[51, 27, 16, 10, 856, 53, 25, 34, 69, 1]

3. Xây dựng RNN

Tổng quan về RNN đã được đề cập trong bài đầu tiên, còn ở đây ta chỉ nói lại tóm tắt để có cái nhìn về cách xây dựng mạng RNN.

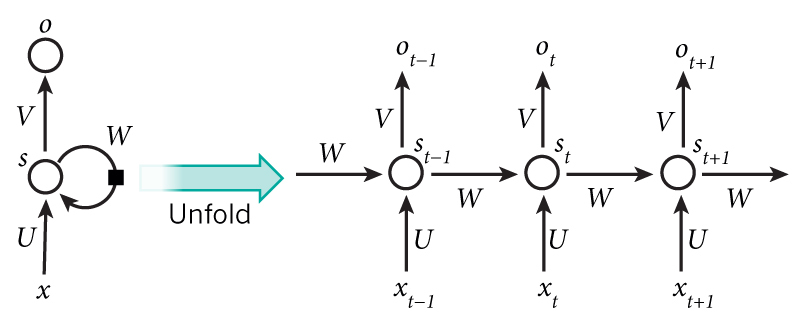A recurrent neural network and the unfolding in time of the computation involved in its forward computation. Source: Nature A recurrent neural network and the unfolding in time of the computation involved in its forward computation. Source: Nature

Hãy nhìn kĩ và để ý xem RNN cho mô hình ngôn ngữ sẽ như thế nào. Đầu vào $ x $ sẽ là một chuỗi các từ và mỗi $ x_t $ sẽ là một từ đơn. Nhưng vì phép nhân ma trận không cho phép ta sử dụng một địa chỉ của từ để làm việc, nên ta phải biểu diễn từ đó bằng véc-tơ one-hot với kích thước là vocabulary_size. Ví dụ, từ có địa chỉ là $ 36 $ thì sẽ có véc-tơ tương ứng là: vị trí thứ $ 36 $ là $ 1 $, còn lại là $ 0 $ cả. Vì mỗi $ x_t $ là một véc-tơ, nên $ x $ lúc này sẽ là một ma trận với mỗi hàng biểu diễn một từ. Ta sẽ thực hiện việc chuyển đổi này ở phần mã mạng nơ-ron chứ không thực hiện ở phần tiền xử lý. Đầu ra của mạng $ o $ cũng sẽ có dạng tương tự. Mỗi $ o_t $ là một véc-tơ có kích cỡ vocabulary_size và mỗi phần tử thể hiện xác xuất xuất hiện kế tiếp của từ tương ứng.

Giờ nhớ lại các công thức của mạng RNN trong bài viết trước:

$$ \begin{aligned} s_t &= \tanh(U x_t + W s_{t-1}) \cr o_t &= \mathrm{softmax}(V s_t) \end{aligned} $$

Tôi thường hay viết ra cỡ của các ma trận và véc-tơ để dễ nhìn thao tác tiện. Giả sử ta chọn lượng từ vựng $ C = 8000 $ và số tầng ẩn là $ H = 100 $ Bạn có thể coi tầng ẩn là bộ nhớ của mạng, càng nhiều tầng ẩn thì ta càng học được nhiều mẫu phức tạp, nhưng đổi lại thời gian tính toán cũng tăng lên. Với trường hợp này, các véc-tơ và ma trận của ta có kích cỡ như sau:

$$ \begin{aligned} x_t &\in \mathbb{R}^{8000} \cr o_t &\in \mathbb{R}^{8000} \cr s_t &\in \mathbb{R}^{100} \cr U &\in \mathbb{R}^{100 \times 8000} \cr V &\in \mathbb{R}^{8000 \times 100} \cr W &\in \mathbb{R}^{100 \times 100} \end{aligned} $$

Những thông tin này cực kì có giá trị trong quá trình xây dựng mạng. $ U $, $ V $ và $ W $ là các tham số của mạng mà ta cần phải học từ tập dữ liệu. Vì vậy, ta sẽ cần học cả thảy là $ 2HC + H^2 $ tham số. Với $ C = 8000 $ và $ H = 100 $ thì tổng số tham số là $ 1,610,000 $. Ngoài ra, các kích cỡ này cho cho ta biết được nút thắt của mô hình khi hoạt động. Lưu ý rằng, vì $ x_t $ là véc-tơ one-hot nên khi nhân nó với $ U $ thì chỉ cần lấy cột tương ứng của $ U $ là được chứ không cần phải thực hiện phép nhân ma trận đầy đủ. Vì vậy, phép nhân lớn nhất của mạng là $ V s_t $, đó chính là lý do mà ta muốn giữ cho lượng từ vựng của ta ít nhất có thể.

Ok, với những vũ khí đó giờ ta bắt đầu thực hiện.

3.1. Khởi tạo

Ta sẽ bắt đầu bằng việc khởi tạo các tham số của mạng trong lớp RNN. Tôi sẽ đặt tên lớp này là RNNNumpy, vì ta sẽ xây dựng một phiên bản Theano sau nữa. Khởi tạo các tham số có chút ràng buộc là không thể để chúng bằng $ 0 $ ngay được. Vì như vậy sẽ làm cho mạng của ta không thể học được. Ta phải khởi tạo chúng một cách ngẫu nhiên. Hiện nay đã có nhiều nghiên cứu chỉ ra việc khởi tạo tham số có ảnh hưởng tới kết quả huấn luyện ra sao. Việc khởi tạo còn phụ thuộc vào hàm kích hoạt (activation function) của ta là gì nữa. Trong trường hợp của ta là hàm $ \tanh $, nên giá trị khởi tạo được khuyến khích nằm trong khoảng $ [ -\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}} ] $. Trong đó, $ n $ là lượng kết nối tới từ tầng mạng trước. Nhìn nó có vẻ phức tạp, nhưng đừng lo lắng nhiều về nó. Chỉ cần bạn khởi tạo các tham số của mình ngẫu nhiên đủ nhỏ thì thường mạng của ta sẽ hoạt động tốt.

rnn_theano.pyrnn_theano.py
1
2
3
4
5
6
7
8
9
10
11
class RNNNumpy:

    def __init__(self, word_dim, hidden_dim=100, bptt_truncate=4):
        # Assign instance variables
        self.word_dim = word_dim
        self.hidden_dim = hidden_dim
        self.bptt_truncate = bptt_truncate
        # Randomly initialize the network parameters
        self.U = np.random.uniform(-np.sqrt(1./word_dim), np.sqrt(1./word_dim), (hidden_dim, word_dim))
        self.V = np.random.uniform(-np.sqrt(1./hidden_dim), np.sqrt(1./hidden_dim), (word_dim, hidden_dim))
        self.W = np.random.uniform(-np.sqrt(1./hidden_dim), np.sqrt(1./hidden_dim), (hidden_dim, hidden_dim))

word_dim ở trên là kích cỡ của tập từ vựng, hidden_dim là số lượng tầng ẩn của ta. Còn bptt_truncate thì ta sẽ giải thích sau.

3.2. Lan truyền tiến

Tiếp theo, ta sẽ cài đặt hàm lan truyền tiến (forward propagation) để thực hiện việc tính xác xuất của từ như sau.

rnn_theano.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def forward_propagation(self, x):
    # The total number of time steps
    T = len(x)
    # During forward propagation we save all hidden states in s because need them later.
    # We add one additional element for the initial hidden, which we set to 0
    s = np.zeros((T + 1, self.hidden_dim))
    s[-1] = np.zeros(self.hidden_dim)
    # The outputs at each time step. Again, we save them for later.
    o = np.zeros((T, self.word_dim))
    # For each time step...
    for t in np.arange(T):
        # Note that we are indxing U by x[t]. This is the same as multiplying U with a one-hot vector.
        s[t] = np.tanh(self.U[:,x[t]] + self.W.dot(s[t-1]))
        o[t] = softmax(self.V.dot(s[t]))
    return [o, s]

RNNNumpy.forward_propagation = forward_propagation

Ở đây, ta không chỉ trả ra kết quả tính toán được mà còn trả ra cả trạng thái ẩn, để phục vụ cho việc tính đạo hàm, việc này tránh cho ta phải tính lại lần nữa khi tính đạo hàm. Mỗi $ o_t $ là một véc-tơ xác xuất của mỗi từ trong danh sách từ vựng của ta, nhưng đôi lúc ta chỉ cần lấy từ có xác xuất cao nhất. Ở đây ta sẽ định nghĩa một hàm dự đoán như sau:

rnn_theano.py
1
2
3
4
5
6
def predict(self, x):
    # Perform forward propagation and return index of the highest score
    o, s = self.forward_propagation(x)
    return np.argmax(o, axis=1)

RNNNumpy.predict = predict

Giờ ta thử chảy các hàm vừa cài đặt xem kết quả ra sao:

train-theano.py
1
2
3
4
5
np.random.seed(10)
model = RNNNumpy(vocabulary_size)
o, s = model.forward_propagation(X_train[10])
print o.shape
print o
(45, 8000)
[[ 0.00012408  0.0001244   0.00012603 ...,  0.00012515  0.00012488
   0.00012508]
 [ 0.00012536  0.00012582  0.00012436 ...,  0.00012482  0.00012456
   0.00012451]
 [ 0.00012387  0.0001252   0.00012474 ...,  0.00012559  0.00012588
   0.00012551]
 ...,
 [ 0.00012414  0.00012455  0.0001252  ...,  0.00012487  0.00012494
   0.0001263 ]
 [ 0.0001252   0.00012393  0.00012509 ...,  0.00012407  0.00012578
   0.00012502]
 [ 0.00012472  0.0001253   0.00012487 ...,  0.00012463  0.00012536
   0.00012665]]

Với mỗi từ trong câu (45 ở trên), mô hình của ta sẽ tính 8000 xác xuất có thể của từ tiếp theo. Chú ý rằng, ta khởi tạo $ U, V, W $ ngẫu nhiên nên lúc này các xác xuất dự đoán được ở trên cũng là ngẫu nhiên. Với đầu ra như vậy, ta có thể lấy địa chỉ của từ có xác xuất cao nhất cho mỗi từ:

train-theano.py
1
2
3
predictions = model.predict(X_train[10])
print predictions.shape
print predictions
(45,)
[1284 5221 7653 7430 1013 3562 7366 4860 2212 6601 7299 4556 2481 238 2539
 21 6548 261 1780 2005 1810 5376 4146 477 7051 4832 4991 897 3485 21
 7291 2007 6006 760 4864 2182 6569 2800 2752 6821 4437 7021 7875 6912 3575]

3.3. Tính lỗi

Để huấn luyện mạng, ta cần phải đánh giá được lỗi cho từng tham số. Và mục tiêu của ta là tìm các tham số $ U, V, W $ để tối thiểu hàm lỗi (loss function) $ L $ của ta trong quá trình huấn luyện. Một trong số các hàm đánh giá lỗi thường được sử dụng là cross-entropy. Nếu ta có $ N $ mẫu huấn luyện (số từ trong văn bản) và $ C $ lớp (số từ vựng) thì lỗi tương ứng với dự đoán $ o $ và nhãn chuẩn $ y $ sẽ là:

$$ L(y, o) = - \frac{1}{N} \sum{y_n \log{o_n}} $$

Công thức trên trông có vẻ hơi phức tạp chút, nhưng tất cả những gì làm là cộng tổng sự khác biệt của từng dự đoán của ta so với thực tế (hay còn gọi là lỗi). Nếu $ y $ (các từ đúng) và $ o $ (các từ dự đoán) càng khác biệt thì lỗi của ta càng lớn. Hàm tính lỗi được cài đặt như sau:

rnn_theano.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def calculate_total_loss(self, x, y):
    L = 0
    # For each sentence...
    for i in np.arange(len(y)):
        o, s = self.forward_propagation(x[i])
        # We only care about our prediction of the "correct" words
        correct_word_predictions = o[np.arange(len(y[i])), y[i]]
        # Add to the loss based on how off we were
        L += -1 * np.sum(np.log(correct_word_predictions))
    return L

def calculate_loss(self, x, y):
    # Divide the total loss by the number of training examples
    N = np.sum((len(y_i) for y_i in y))
    return self.calculate_total_loss(x,y)/N

RNNNumpy.calculate_total_loss = calculate_total_loss
RNNNumpy.calculate_loss = calculate_loss

Giờ nhìn lại một chút và nghĩ xem lỗi sẽ thế nào với các tham số được khởi tạo ngẫu nhiên. Nó sẽ giúp ta đảm bảo được việc cài đặt của ta là chính xác. Ta có $ C $ từ trong tập từ vựng, vì vậy mỗi từ sẽ có dự đoán trung bình là $ {1}/{C} $, nên lỗi của ta sẽ là $ L = - \frac{1}{N} N \log{\frac{1}{C}} = \log{C} $.

rnn_theano.py
1
2
3
# Limit to 1000 examples to save time
print "Expected Loss for random predictions: %f" % np.log(vocabulary_size)
print "Actual loss: %f" % model.calculate_loss(X_train[:1000], y_train[:1000])
Expected Loss for random predictions: 8.987197
Actual loss: 8.987440

Có vẻ khá gần với kết quả chuẩn xác rồi! Cũng nói luôn rằng việ đánh giá lỗi cho toàn bộ tập dữ liệu là một thao tác tốn kém, có thể mất tới hàng giờ đồng hồ tùy thuộc vào lượng dữ liệu mà ta đưa vào huấn luyện.

3.4. Huấn luyện RNN với SGD và BPTT

Nhớ lại rằng, ta cần tìm các tham số $ U, V, W $ sao cho tổng lỗi của ta là nhỏ nhất với tập dữ liệu huấn luyện. Cách phổ biến nhất là sử dụng SGD (Stochastic Gradient Descent - trượt đồi). Ý tưởng đằng sau SGD khác đơn giản. Ta sẽ lặp đi lặp lại suốt tập dữ liệu của ta và tạo mỗi bước lặp ta sẽ thay đổi tham số của ta sao cho tổng lỗi có thể giảm đi. Hướng của việc cập nhập tham số được tính dựa vào đạo hàm của hàm lỗi: $\displaystyle \frac{\partial{L}}{\partial{U}}, \frac{\partial{L}}{\partial{V}}, \frac{\partial{L}}{\partial{W}} $. Để thực hiện SGD, ta cần phải có độ học (learning rate) để xác định các mức độ thay đổi tham số của ta ở mỗi bước lặp. SGD không chỉ là phương thức tối ưu phổ biến nhất trong mạng nơ-ron mà còn trong nhiều giải thuật học máy khác nữa. Cho tới thời điểm này, ta có rất nhiều các nghiên cứu làm sao để tối ưu SGD bằng cách sử dụng các lô dữ liệu, bằng cách song song hoá và thay đổi tham số học trong quá trình huấn luyện. Thậm chí với nhiều ý tưởng đơn giản để thực hiện SGD một cách hiệu quả cũng khiến nó trở lên rất phức tạp để cài đặt. Trên mạng hiện có rất nhiều bài hướng dẫn về SGD, nên tôi sẽ không bàn cụ thể nó ở đây nữa. Tôi sẽ chỉ cài đặt phiên bản đơn giản của SGD để cho cả các bạn không có kiến thức về tối ứu hoá có thể dễ nắm bắt được vấn đề.

Làm sao ta có thể tính được đạo hàm như ta vừa đề cập phía trên? Trong các mạng nơ-ron truyền thống, ta sẽ làm việc đó bằng giải thuật lan truyền ngược (backpropagation algorithm). Nhưng với mạng RNN, ta sử dụng phiên bản hơi khác của giải thuật này là lan truyền ngược liên hồi - BPTT (Backpropagation Through Time). Vì các tham số được chia sẻ chung trong suốt các bước trong mạng, nên đạo hàm tại mỗi đầu ra phụ thuộc không chỉ vào kết quả tính hiện tại mà còn phụ thuộc vào các các tính toán ở bước trước. Nếu bạn biết đại số tuyến tính, nó giống như việc ứng dụng quy tắc chuỗi (chain rule). Ở bài này, tôi không trình bày chi tiết về BPTT, mà sẽ dành nó cho bài viết tới. Ngoài ra, bạn có thể tham khảo thêm về giải thuật lan truyền ngược tại đây và đây nữa. Giờ bạn có thể coi BPTT là một hộp đen đi nhé. Hộp đen này nhận tham số đầu vào là tập mẫu huấn luyện $ (x, y) $ và trả ra đạo hàm: $\displaystyle \frac{\partial{L}}{\partial{U}}, \frac{\partial{L}}{\partial{V}}, \frac{\partial{L}}{\partial{W}} $.

rnn_theano.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def bptt(self, x, y):
    T = len(y)
    # Perform forward propagation
    o, s = self.forward_propagation(x)
    # We accumulate the gradients in these variables
    dLdU = np.zeros(self.U.shape)
    dLdV = np.zeros(self.V.shape)
    dLdW = np.zeros(self.W.shape)
    delta_o = o
    delta_o[np.arange(len(y)), y] -= 1.
    # For each output backwards...
    for t in np.arange(T)[::-1]:
        dLdV += np.outer(delta_o[t], s[t].T)
        # Initial delta calculation
        delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ** 2))
        # Backpropagation through time (for at most self.bptt_truncate steps)
        for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:
            # print "Backpropagation step t=%d bptt step=%d " % (t, bptt_step)
            dLdW += np.outer(delta_t, s[bptt_step-1])              
            dLdU[:,x[bptt_step]] += delta_t
            # Update delta for next step
            delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
    return [dLdU, dLdV, dLdW]

RNNNumpy.bptt = bptt

3.5. Kiểm tra đạo hàm

Khi cài đặt thuật toán lan truyền ngược thì cũng nên cài đặt luôn phép kiểm tra đạo hàm (gradient checking) để kiểm chứng rằng giải thuật ta cài đặt không bị sai. Ý tưởng đằng sau phép kiểm tra đạo hàm là đạo hàm riêng của mỗi tham số tương đương với độ dốc tại điểm đó. Vì vậy ta có thể thay đổi giá tham số một chút rồi chia cho khoảng thay đổi đó để được sấp sỉ đạo hàm riêng theo tham số đó.

$$ \frac{\partial{L}}{\partial{\theta}} \approx \lim\limits_{h \to 0}{\frac{J(\theta + h) - J(\theta - h)}{2h}} $$

Sau đó ta sẽ kiểm tra đạo hảm thu được bằng giải thuật lan truyền ngược với giá trị thu được ở công thức trên. Nếu sự khác biệt không lớn thì giải thuật vừa cải đặt là chấp nhận được. Ta cần phải tính đạo hàm riêng bằng công thức trên cho tất cả các tham số, nên việc kiểm tra đạo hàm cũng là một thao tác tốn kém (lưu ý rằng ta có tới hơn một triệu tham số ở ví dụ trên nhé). Nên trong thực tế ta chỉ cần thực hiện phép kiểm định đó trên một tập từ vựng nhỏ hơn thực tế.

rnn_theanornn_theano.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def gradient_check(self, x, y, h=0.001, error_threshold=0.01):
    # Calculate the gradients using backpropagation. We want to checker if these are correct.
    bptt_gradients = self.bptt(x, y)
    # List of all parameters we want to check.
    model_parameters = ['U', 'V', 'W']
    # Gradient check for each parameter
    for pidx, pname in enumerate(model_parameters):
        # Get the actual parameter value from the mode, e.g. model.W
        parameter = operator.attrgetter(pname)(self)
        print "Performing gradient check for parameter %s with size %d." % (pname, np.prod(parameter.shape))
        # Iterate over each element of the parameter matrix, e.g. (0,0), (0,1), ...
        it = np.nditer(parameter, flags=['multi_index'], op_flags=['readwrite'])
        while not it.finished:
            ix = it.multi_index
            # Save the original value so we can reset it later
            original_value = parameter[ix]
            # Estimate the gradient using (f(x+h) - f(x-h))/(2*h)
            parameter[ix] = original_value + h
            gradplus = self.calculate_total_loss([x],[y])
            parameter[ix] = original_value - h
            gradminus = self.calculate_total_loss([x],[y])
            estimated_gradient = (gradplus - gradminus)/(2*h)
            # Reset parameter to original value
            parameter[ix] = original_value
            # The gradient for this parameter calculated using backpropagation
            backprop_gradient = bptt_gradients[pidx][ix]
            # calculate The relative error: (|x - y|/(|x| + |y|))
            relative_error = np.abs(backprop_gradient - estimated_gradient)/(np.abs(backprop_gradient) + np.abs(estimated_gradient))
            # If the error is to large fail the gradient check
            if relative_error > error_threshold:
                print "Gradient Check ERROR: parameter=%s ix=%s" % (pname, ix)
                print "+h Loss: %f" % gradplus
                print "-h Loss: %f" % gradminus
                print "Estimated_gradient: %f" % estimated_gradient
                print "Backpropagation gradient: %f" % backprop_gradient
                print "Relative Error: %f" % relative_error
                return
            it.iternext()
        print "Gradient check for parameter %s passed." % (pname)

RNNNumpy.gradient_check = gradient_check
train-theano
1
2
3
4
5
# To avoid performing millions of expensive calculations we use a smaller vocabulary size for checking.
grad_check_vocab_size = 100
np.random.seed(10)
model = RNNNumpy(grad_check_vocab_size, 10, bptt_truncate=1000)
model.gradient_check([0,1,2,3], [1,2,3,4])

3.6. Thực hiện SGD

Giờ ta đã có thể tính được đạo hàm cho từng tham số nên có thể cài đặt được SGD. Ta sẽ thực hiện nó qua 2 bước: 1. Xây dựng hàm sdg_step để tính đạo hàm và thực hiện việc cập nhập cho mỗi lô dữ liệu. 2. Chạy một vòng lặp bên ngoài suốt toàn bộ tập dữ liệu và điều chỉnh độ học.

train-theano.py
1
2
3
4
5
6
7
8
9
10
# Performs one step of SGD.
def numpy_sdg_step(self, x, y, learning_rate):
    # Calculate the gradients
    dLdU, dLdV, dLdW = self.bptt(x, y)
    # Change parameters according to gradients and learning rate
    self.U -= learning_rate * dLdU
    self.V -= learning_rate * dLdV
    self.W -= learning_rate * dLdW

RNNNumpy.sgd_step = numpy_sdg_step
train-theano.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Outer SGD Loop
# - model: The RNN model instance
# - X_train: The training data set
# - y_train: The training data labels
# - learning_rate: Initial learning rate for SGD
# - nepoch: Number of times to iterate through the complete dataset
# - evaluate_loss_after: Evaluate the loss after this many epochs
def train_with_sgd(model, X_train, y_train, learning_rate=0.005, nepoch=100, evaluate_loss_after=5):
    # We keep track of the losses so we can plot them later
    losses = []
    num_examples_seen = 0
    for epoch in range(nepoch):
        # Optionally evaluate the loss
        if (epoch % evaluate_loss_after == 0):
            loss = model.calculate_loss(X_train, y_train)
            losses.append((num_examples_seen, loss))
            time = datetime.now().strftime('%Y-%m-%d %H:%M:%S')
            print "%s: Loss after num_examples_seen=%d epoch=%d: %f" % (time, num_examples_seen, epoch, loss)
            # Adjust the learning rate if loss increases
            if (len(losses) > 1 and losses[-1][1] > losses[-2][1]):
                learning_rate = learning_rate * 0.5
                print "Setting learning rate to %f" % learning_rate
            sys.stdout.flush()
        # For each training example...
        for i in range(len(y_train)):
            # One SGD step
            model.sgd_step(X_train[i], y_train[i], learning_rate)
            num_examples_seen += 1

Ok rồi! Giờ để xem mô hình chạy mất bao lâu để học nhé.

train-theano.py
1
2
3
np.random.seed(10)
model = RNNNumpy(vocabulary_size)
%timeit model.sgd_step(X_train[10], y_train[10], 0.005)

Hự, toi thật. Mỗi bước của SGD chạy mất xấp xỉ 350 mili giây trên máy tính của tôi. Ta có tới 80,000 mẫu trong tập dữ liệu huấn luyện, nên mỗi vòng lặp mất tới vài giờ để thực hiện. Nhiều vòng lặp sẽ mất mấy ngày mất, thậm chí cả vài tuần mới chạy xong được. Ở đây ta mới chỉ chạy với một tập dữ liệu nhỏ thôi đấy, chứ nhiều công ty hay các nhà nghiên cứu khác họ chạy với tập dữ liệu lớn hơn rất nhiều. Làm thế nào giờ?

May mắn là có nhiều cách để tăng tốc chương trình của ta. Ta có thể giữ nguyên mô hình và làm cho mã nguồn ta chạy nhanh hơn, hoặc thay đổi mô hình để việc tính toán bớt tốn kém đi, hoặc là làm cả 2 việc đó. Các nhà nghiên cứu đã đưa ra được nhiều cách để mô hình của ta giảm bớt được chi phí tính toán, ví dụ như sử dụng softmax phân cấp hay thêm các tầng chiếu để tránh việc nhân các ma trạn lớn. (bạn có thể tham khảo chi tiết tại đây và đây). Nhưng tôi vẫn muốn giữ cho mô hình của ta đơn giản, nên tôi sẽ cho chạy trên GPU. Trước khi làm việc này, ta hay thử chạy SGD với một tập dữ liệu nhỏ và kiểm tra xem lỗi có thực sự giảm sau mỗi vòng lặp hay không.

train-theano.py
1
2
3
4
np.random.seed(10)
# Train on a small subset of the data to see what happens
model = RNNNumpy(vocabulary_size)
losses = train_with_sgd(model, X_train[:100], y_train[:100], nepoch=10, evaluate_loss_after=1)
2015-09-30 10:08:19: Loss after num_examples_seen=0 epoch=0: 8.987425
2015-09-30 10:08:35: Loss after num_examples_seen=100 epoch=1: 8.976270
2015-09-30 10:08:50: Loss after num_examples_seen=200 epoch=2: 8.960212
2015-09-30 10:09:06: Loss after num_examples_seen=300 epoch=3: 8.930430
2015-09-30 10:09:22: Loss after num_examples_seen=400 epoch=4: 8.862264
2015-09-30 10:09:38: Loss after num_examples_seen=500 epoch=5: 6.913570
2015-09-30 10:09:53: Loss after num_examples_seen=600 epoch=6: 6.302493
2015-09-30 10:10:07: Loss after num_examples_seen=700 epoch=7: 6.014995
2015-09-30 10:10:24: Loss after num_examples_seen=800 epoch=8: 5.833877
2015-09-30 10:10:39: Loss after num_examples_seen=900 epoch=9: 5.710718

Tốt, có vẻ như ta cài đặt nó không sai và lỗi đang được giảm đi rồi.

4. Huấn luyện với Theano trên GPU

Tôi có viết một bài về Theano, về cơ bản lô-gíc vẫn như vậy, nên thôi sẽ bỏ qua việc tối ưu mã nguồn ở đây. Tôi định nghĩa một lớp RNNTheano để thay thế các phép tính numpy tương ứng bằng phép tính của Theano. Cụ thể bạn có thể xem trên Github nhé.

train-theano.py
1
2
3
np.random.seed(10)
model = RNNTheano(vocabulary_size)
%timeit model.sgd_step(X_train[10], y_train[10], 0.005)

Lúc này, mỗi bước SGD chạy mất 70ms trên máy Mac của tôi (không có GPU) và 23ms trên g2.2xlarge của Amazon EC2 với GPU. Nhanh hơn 15 lần so với cách chạy đầu của ta và có nghĩa là ta có thể huấn luyện mô hình của ta trong vài giờ hoặc vài ngày thay vì hàng tuần trời. Vẫn có nhiều cách tối ưu hoá khác mà ta có thể làm, nhưng hiện tại cứ để đó đã.

Để tránh việc bạn mấy hàng ngày trời để huấn luyện mô hình, tôi có huấn luyện sẵn một mô hình Theano với 50 tầng ẩn và 8,000 từ vựng. Tôi đã huấn luyện nó với 50 vòng lặp trong 20 giờ :D . Tuy vậy lỗi vẫn tiếp tục giảm dần, nên một cách trực quan ta có thể nghĩ rằng nếu huấn luyện thêm nữa thì kết quả sẽ tốt hơn. Nhưng mà thôi, mất thời gian lắm vì tôi cũng muốn đưa bài này ra lò sớm :D Tuy nhiên, bạn có thể thử huấn luyện nó lâu hơn xem sao đi nhé. Bạn có thể lấy các tham số của mô hình trong phần data/trained-model-theano.npz trên Github về rồi chạy nó như sau:

train-theano.py
1
2
3
4
5
6
from utils import load_model_parameters_theano, save_model_parameters_theano

model = RNNTheano(vocabulary_size, hidden_dim=50)
# losses = train_with_sgd(model, X_train, y_train, nepoch=50)
# save_model_parameters_theano('./data/trained-model-theano.npz', model)
load_model_parameters_theano('./data/trained-model-theano.npz', model)

5. Sinh văn bản

Giờ ta đã có mô hình và ta có thể nhờ nó sinh ra văn bản mới cho ta rồi. Đoạn mã dưới đây là một hàm dùng để sinh ra các câu mới.

train-theano.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def generate_sentence(model):
    # We start the sentence with the start token
    new_sentence = [word_to_index[sentence_start_token]]
    # Repeat until we get an end token
    while not new_sentence[-1] == word_to_index[sentence_end_token]:
        next_word_probs = model.forward_propagation(new_sentence)
        sampled_word = word_to_index[unknown_token]
        # We don't want to sample unknown words
        while sampled_word == word_to_index[unknown_token]:
            samples = np.random.multinomial(1, next_word_probs[-1])
            sampled_word = np.argmax(samples)
        new_sentence.append(sampled_word)
    sentence_str = [index_to_word[x] for x in new_sentence[1:-1]]
    return sentence_str

num_sentences = 10
senten_min_length = 7

for i in range(num_sentences):
    sent = []
    # We want long sentences, not sentences with one or two words
    while len(sent) < senten_min_length:
        sent = generate_sentence(model)
    print " ".join(sent)

Dưới đây là một số câu được sinh ra:

  • Anyway, to the city scene you’re an idiot teenager.
  • What ? ! ! ! ! ignore!
  • Screw fitness, you’re saying: https
  • Thanks for the advice to keep my thoughts around girls.
  • Yep, please disappear with the terrible generation.

Nhìn vào các câu được sinh ra, ta có thể thu được vài thứ đáng lưu tâm ở đây. Mô hình của ta đã học được cách sử dụng cú pháp câu thành công, nó thêm được các dấu phẩy (and’s và or’s) và chấm hếtcaau nữa. Đôi lúc nó còn thêm được cả các dấu chấm cảm và mặt cười như các bình luận trên SNS.

Tuy nhiên vẫn các câu sinh ra vẫn gặp một điểm yếu lớn là ngữ pháp chưa chính xác (các câu ở trên là tôi đã nhặt các câu tốt nhất rồi đó). Một lý do có thể là do ta chưa huấn luyện nó đủ lâu, nhưng hình như đó không phải là lý do chính. RNN thuần không thể sinh được các câu có nghĩa vì nó không thể học được các phụ thuộc giữa các từ cách xa nhau. Đó cũng là lý do mà RNN không được ưu chuộng khi nó được sáng tạo ra. Về mặt lý thuyết trông nó rất đẹp, nhưng nó lại không chạy tốt trong thực tế và lúc đó ta cũng không biết tại sao ngay được.

May mắn là hiện nay sự khó khăn khi huấn luyện RNN đã được lý giải giúp ta hiểu hơn. Trong phần tiếp theo của chuỗi bài này, ta sẽ khám phá giải thuật lan truyền ngược liên hồi BPTT (Backpropagation Through Time) chi tiết và xem xét vấn đề mất mát đạo hàm của nó (vanishing gradient problem). Đó là điểm khởi nguyên để ta có nhiều mô hình RNN tốt hơn như LSTM chẳng hạn. LSTM hiện này là một phương pháp chính được sử dụng cho rất nhiều bài toán NPL (và có thể sinh ra các bình luận Reddit hợp lý hơn). Tất cả những điều bạn học được trong phần này sẽ được áp dụng cho LSTM và các mô hình RNN khác nữa, nên đừng cảm thấy thất vọng ngay với kết quả của RNN thuần thu được.

Tôi xin dừng bài viết tại đây, nếu bạn có khúc mắc hay góp ý gì thì hãy bình luận ở phía dưới nhé. Cũng đừng quên xem mã nguồn đầy đủ trên Github ha.