Bài giới thiệu RNN thứ 3 này được dịch lại từ trang blog WILDML.

Trong phần này tôi sẽ giới thiệu tổng quan về BPTT (Backpropagation Through Time) và giải thích sự khác biệt của nó so với các giải thuật lan truyền ngược truyền thống. Sau đó ta sẽ cùng tìm hiểu vấn đề mất mát đạo hàm (vanishing gradient problem), nó dẫn ta tới việc phát triển của LSTM và GRU - 2 mô hình phổ biến và mạnh mẽ nhất hiện nay trong các bài toán NLP (và cả các lĩnh vực khác).

Vấn đề mất mát đạo hàm được khám phá bởi Sepp Hochreiter năm 1991 và đã cuốn hút được sự quan tâm cho lần nữa trong thời gian gần đây khi mà ứng dụng của các kiến trúc sâu ngày một nhiều hơn.

Đây là bài thứ 3 trong chuỗi bài giới thiệu về RNN:

Để có thể hiểu được toàn bộ bài viết này, bạn cần có kiến thức về giải tích và cơ bản về giải thuật lan truyền ngược (backpropagation). Nếu bạn chưa rõ nó thì có thể đọc tại các bài viết này và này và cả đây nữa (thứ tự khó dần nhé).

Mục lục

1. Lan truyền ngược liên hồi - BPTT

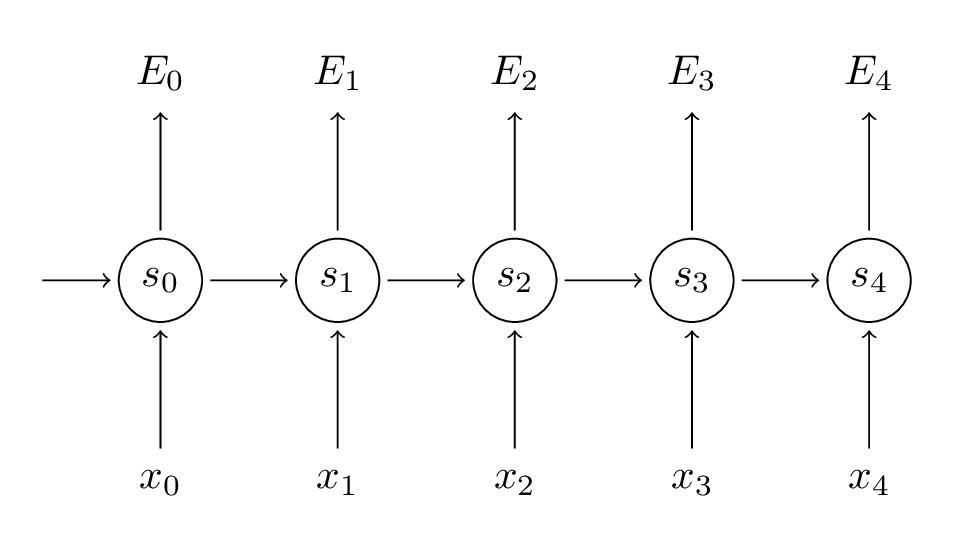
Nhớ lại chút các công thức cơ bản của RNN. Lưu ý rằng các kí hiệu ở đây có thay đổi 1 chút từ $ o $ thành $ \hat{y} $. Việc thay đổi này nhằm thống nhất với một vài tài liệu tôi sẽ tham chiếu tới.

$$ \begin{aligned} s_t &= \tanh(U x_t + W s_{t-1}) \cr \hat{y_t} &= \mathrm{softmax}(V s_t) \end{aligned} $$

Ta cũng định nghĩa hàm mất mát, hay hàm lỗi dạng cross entropy như sau:

$$ \begin{aligned} E_t(y_t, \hat{y_t}) &= -y_t \log{\hat{y_t}} \cr E(y, \hat{y}) &= \sum_t{E_t(y_t, \hat{y_t})} \cr \ &= -\sum_t{y_t \log{\hat{y_t}}} \end{aligned} $$

Ở đây, $ y_t $ là từ chính xác ở bước $ t $, còn $ \hat{y_t} $ là từ mà ta dự đoán. Ta coi mỗi chuỗi đầy đủ (một câu) là một mẫu huấn luyện. Vì vậy tổng số lỗi chính là tổng của tất cả các lỗi ở mỗi bước (mỗi từ).

Mục tiêu của ta là tính đạo hàm của lỗi với tham số $ U, V, W $ tương ứng và sau đó học các tham số này bằng cách sử dụng SGD. Tương tự như việc cộng tổng các lỗi, ta cũng sẽ cộng tổng các đạo hàm tại mỗi bước cho mỗi mẫu huấn luyện: $\displaystyle \frac{\partial{E}}{\partial{W}} = \sum_t{\frac{\partial{E_t}}{\partial{W}}} $.

Để tính đạo hàm, ta sử dụng quy tắc chuỗi vi phân. Quy tắc này được áp dụng cho việc truyền ngược lỗi của giải thuật lan truyền ngược.

$$ \begin{aligned} \frac{\partial{E_3}}{\partial{V}} &= \frac{\partial{E_3}}{\partial{\hat{y_3}}} \frac{\partial{\hat{y_3}}}{\partial{V}} \cr \ &= \frac{\partial{E_3}}{\partial{\hat{y_3}}} \frac{\partial{\hat{y_3}}}{\partial{z_3}} \frac{\partial{z_3}}{\partial{V}} \cr \ &= (\hat{y_3} - y_3) \otimes s_3 \end{aligned} $$

Trong đó, $ z_3 = V s_3 $ và $ \otimes $ là phép nhân ngoài của 2 véc-tơ . Nếu bạn không hiểu phép khai triển trên thì cũng đừng lo lắng gì cả, tôi có bỏ qua 1 vài bước khi khai triển, nếu cần thiết bạn có thể tự tính đạo hàm xem khớp hay không. Qua phép khai triển trên, tôi chỉ muốn nói 1 điều là $\displaystyle \frac{\partial{E_3}}{\partial{V}} $ chỉ phụ thuộc vào các giá trị ở bước hiện thời: $ \hat{y_3}, y_3, s_3 $ mà thôi. Nhìn vào công thức đó, ta thấy rằng tính đạo hàm cho $ V $ chỉ đơn giản là phép nhân ma trận.

Nhưng với $ W $ và $ U $ thì phép tính của ta lại không đơn giản như vậy.

$$ \frac{\partial{E_3}}{\partial{W}} = \frac{\partial{E_3}}{\partial{\hat{y_3}}} \frac{\partial{\hat{y_3}}}{\partial{s_3}} \frac{\partial{s_3}}{\partial{W}} $$

Với $ s_3 = \tanh{U x_t + W s_2} $ phụ thuộc vào $ s_2 $, còn $ s_2 $ lại phụ thuộc vào $ W $ và $ s_1 $,… Vì vậy với W, ta không thể nào coi $ s_2 $ là hẳng số để tính toán như với $ V $ được. Ta tiếp tục áp dụng quy tắc chuỗi xem sao:

$$ \frac{\partial{E_3}}{\partial{W}} = \frac{\partial{E_3}}{\partial{\hat{y_3}}} \frac{\partial{\hat{y_3}}}{\partial{s_3}} \frac{\partial{s_3}}{\partial{s_k}} \frac{\partial{s_k}}{\partial{W}} $$

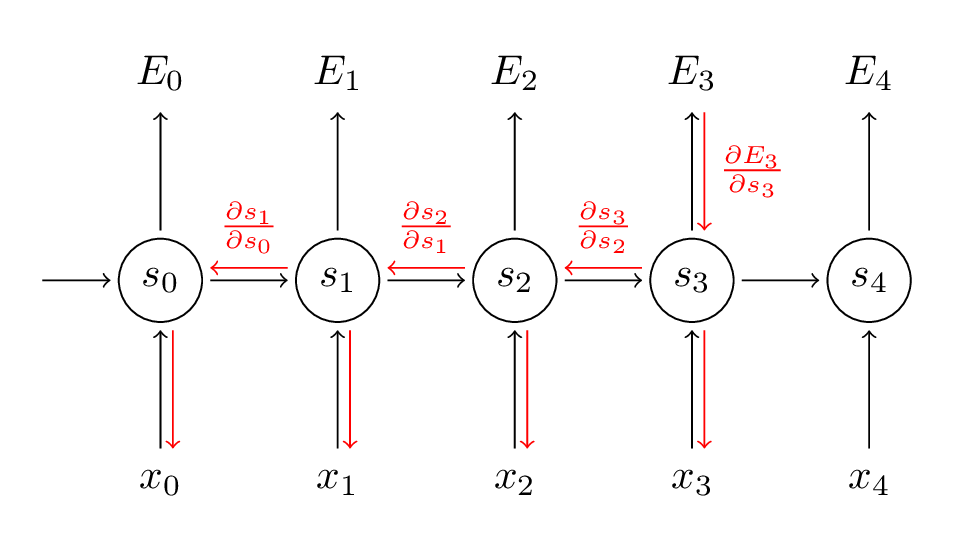
Như vậy, với W ta phải cộng tổng tất cả các đầu ra ở các bước trước để tính được đạo hàm. Nói cách khác, ta phải truyền ngược đạo hàm từ $ t = 3 $ về tới $ t = 0 $.

Cách làm này cũng giống hệt như giải thuật truyền ngược chuẩn trong mạng nơ-ron truyền thống. Điểm khác ở đây là ta cộng tổng các đạo hàm của W tại mỗi bước thời gian. Trong mạng nơ-ron truyền thống, ta không chia sẻ các tham số cho các tầng mạng, nên ta không cần phải cộng tổng đạo hàm lại với nhau. Cũng tương tự như với lan truyền ngược truyền thống, ta có thể định nghĩa véc-tơ delta khi lan truyền ngược lại: $\displaystyle \delta_x^{(3)} = \frac{\partial{E_3}}{\partial{z_2}} = \frac{\partial{E_3}}{\partial{s_3}} \frac{\partial{s_3}}{\partial{s_2}} \frac{\partial{s_2}}{\partial{z_2}} $ với $ z_2 = U x_2 + W s_1 $. Các công thức tính toán tiếp theo hoàn toàn có thể dạng dụng tương tự.

Dưới đây là mà nguồn thực hiện BPTT:

bptt.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def bptt(self, x, y):
    T = len(y)
    # Perform forward propagation
    o, s = self.forward_propagation(x)
    # We accumulate the gradients in these variables
    dLdU = np.zeros(self.U.shape)
    dLdV = np.zeros(self.V.shape)
    dLdW = np.zeros(self.W.shape)
    delta_o = o
    delta_o[np.arange(len(y)), y] -= 1.
    # For each output backwards...
    for t in np.arange(T)[::-1]:
        dLdV += np.outer(delta_o[t], s[t].T)
        # Initial delta calculation: dL/dz
        delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ** 2))
        # Backpropagation through time (for at most self.bptt_truncate steps)
        for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:
            # print "Backpropagation step t=%d bptt step=%d " % (t, bptt_step)
            # Add to gradients at each previous step
            dLdW += np.outer(delta_t, s[bptt_step-1])              
            dLdU[:,x[bptt_step]] += delta_t
            # Update delta for next step dL/dz at t-1
            delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
    return [dLdU, dLdV, dLdW]

Nhìn vào đây, ta có thể biết được phần nào mạng RNN chuẩn khó để huấn luyện, vì các chuỗi (câu) có thể khá dài đến tận 20 từ thậm chí nhiều hơn thế nên ta cần phải truyền ngược lại thông qua rất nhiều tầng mạng. Trong thực tế, người ta sẽ bỏ qua một vài bước truyền ở một số bước.

2. Vấn đề mất mát đạo hàm

Với các câu dài RNN không thể liên kết được các từ ở cách xa nhau nên việc học các câu dài sẽ bị thất bại. Vậy nguyên nhân là gì, ta cùng bắt đầu tìm hiểu từ công thức tính đạo hàm:

$$ \frac{\partial{E_3}}{\partial{W}} = \sum_{k=0}^3{ \frac{\partial{E_3}}{\partial{\hat{y_3}}} \frac{\partial{\hat{y_3}}}{\partial{s_3}} \frac{\partial{s_3}}{\partial{s_k}} \frac{\partial{s_k}}{\partial{W}} } $$

Ở đây, $\displaystyle \frac{s_3}{s_k} $ cũng tuân theo quy tắc chuỗi đạo hàm. Ví dụ: $\displaystyle \frac{s_3}{s_1} = \frac{s_3}{s_2} \frac{s_2}{s_1} $. Nếu bạn để ý thì sẽ thấy các thành phần ở công thức trên đều là véc-tơ vì phép lấy đạo hàm cho véc-tơ cũng là véc-tơ, nên kết quả thu được sẽ là một ma trận (ma trận Jacobi), trong đó các phần tử tương ứng được tính theo phép toán pointwise với đạo hàm tương ứng. Ta có thể viết lại công thức trên như sau:

$$ \frac{\partial{E_3}}{\partial{W}} = \sum_{k=0}^3{ \frac{\partial{E_3}}{\partial{\hat{y_3}}} \frac{\partial{\hat{y_3}}}{\partial{s_3}} \Bigg( \prod_{j=k+1}^3{ \frac{\partial{s_j}}{\partial{s_{j-1}}} } \Bigg) \frac{\partial{s_k}}{\partial{W}} } $$

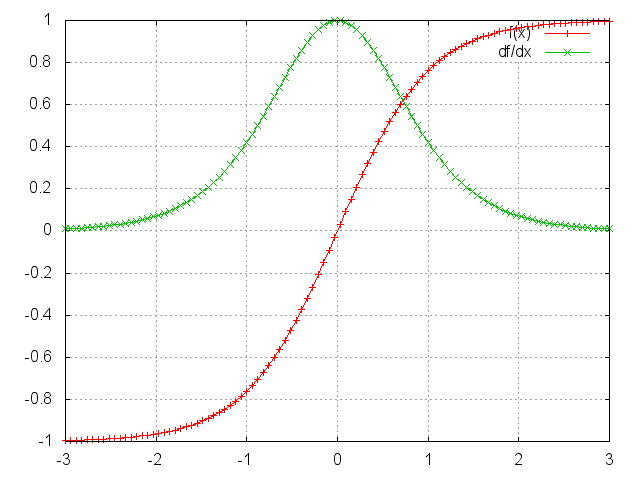
Tôi không chứng minh ở đây (bạn có thể xem ở đây), nhưng phép tính trên cho ta một norm bậc 2. Bạn có thể coi nó là một giá trị tuyệt đối có biên trên là 1 của ma trận Jacobi ở trên. Vì hàm kích hoạt ($ \tanh $ hay $ sigmoid $) của ta sẽ cho kết quả đầu ra nằm trong đoạn $ [-1, 1] $ nên đạo hàm của nó sẽ bị đóng trong khoảng $ [0, 1] $ (với $ sigmoid $ thì giá trị sẽ là $ [0, 0.25] $).

tanh and derivative. Source: http://nn.readthedocs.org/en/rtd/transfer/ tanh and derivative. Source: http://nn.readthedocs.org/en/rtd/transfer/

Nhìn vào hình trên, bạn có thể cả hàm $ \tanh $ lẫn $ sigmoid $ sẽ có đạo hàm bằng $ 0 $ tại 2 đầu. Mà khi đạo hàm bằng 0 thì nút mạng tương ứng tại đó sẽ bị bão hòa. Lúc đó các nút phía trước cũng sẽ bị bão hoà theo. Nên với các giá trị nhỏ trong ma trận, khi ta thực hiện phép nhân ma trận sẽ đạo hàm tương ứng sẽ bùng nổi rất nhanh, thậm chí nó sẽ bị triệt tiêu chỉ sau vài bước nhân. Như vậy, các bước ở xa sẽ không còn tác dụng với nút hiện tại nữa, làm cho RNN không thể học được các phụ thuộc xa. Vấn đề này không chỉ xảy ra với mạng RNN mà ngay cả mạng nơ-ron chuẩn khá sâu cũng có hiện tượng này. Như bạn đã biết RNN cũng là một mạng chuẩn sâu, với số tầng mạng bằng với số từ đầu vào của một chuỗi, nên hiện tượng này có thể thấy ngay ở RNN.

Với cách nhìn như trên ta có thể suy luận thêm vấn đề bùng nổ đạo hàm của RNN nữa. Tùy thuộc vào hàm kích hoạt và tham số của mạng, vấn đề bùng nổ đạo hàm có thể xảy ra khi các giá trị của ma trận là lớn. Tuy nhiên, người ta thường nói về vấn đề mất mát đạo hàm nhiều hơn là bùng nổ đạo hàm, vì 2 lý do sau. Thứ nhất, bùng nổ đạo hàm có thể theo dõi được vì khi đạo hàm bị bùng nổ thì ta sẽ thu được kết quả là một giá trị phi số NaN làm cho chương trình của ta bị dừng hoạt động. Lý do thứ 2 là bùng nổ đạo hàm có thể ngăn chặn được khi ta đặt một ngưỡng giá trị trên cho đạo hàm như trong bài viết này. Còn việc mất mát đạo hàm lại không theo dõi được mà cũng không biết làm sao để xử lý nó cho hợp lý.

May mắn là giờ đã có nhiều nghiên cứu chỉ ra các cách giải quyết vấn đề này. Ví dụ như việc khởi tạo tham số $ W $ hợp lý sẽ giúp giảm được hiệu ứng mất mát đạo hàm. Một phương pháp được ưu chuộng hơn là thay vì sử dụng $ \tanh $ và $ sigmoid $ cho hàm kích hoạt thì ta sử dụng $ ReLU $. Đạo hàm ReLU sẽ là một số hoặc là 0 hoặc là 1, nên có ta có thể kiểm soát được vấn đề mất mát đạo hàm. Một phương pháp phổ biến hơn cả là sử dụng kiến trúc nhớ dài-ngắn hạn (LSTM - Long Short-Term Memory) hoặc Gated Recurrent Unit (GRU). LSTM được đề xuất vào năm 1997 và có lẽ giờ nó là phương pháp phổ biến nhất trong lĩnh vực NLP. Còn GRU mới được giới thiệu vào năm 2014, nó là một phiên bản đơn giản hoá của LSTM. Cả 2 kiến trúc RNN đó được thiết kế để tránh vấn đề mất mát đạo hàm và hiệu quả cho việc học các phụ thuộc xa. Giờ tôi sẽ dừng bài viết tại đây để dành phần giới thiệu 2 kiến trúc đó ở bài viết sau.