Bài này sẽ tập trung vào lý thuyết đằng sau các lỗi mô hình đã trình bày ở bài viết trước. Việc hiểu lý thuyết này giúp ta có được cái nhìn toàn vẹn hơn về lỗi mô hình và cơ sở đánh giá lỗi.

Mục lục

1. Phân tích kỳ vọng lỗi

Giả sử ta có $y=f(\mathbf{x})+\mathcal{N}(0,\sigma^2)$ là đầu ra thực tế ứng với mỗi đầu vào $\mathbf{x}$. Giờ ta cần tìm $\hat{f}(\mathbf{x},\theta)$ xấp xỉ với $f(\mathbf{x})$ nhất có thể bằng cách học tham số $\theta$.

$$E[L]=E[\big(y-\hat{f}(\mathbf{x})\big)^2]=\iint\big(\hat{f}(\mathbf{x})-y\big)^2p(\mathbf{x},y)\text{d}\mathbf{x}\text{d}y$$

Về cơ bản đây cũng chính là trung bình lỗi $J(\theta)$ với nhiều tập dữ liệu, hay nói cách khác là trung bình lỗi cho cả những dữ liệu mà ta chưa có được. Như vậy, rất hiển nhiên là muốn mô hình của ta hoạt động tốt thì kỳ vọng lỗi này phải là nhỏ nhất có thể.

Ở đây tôi không chứng minh, nhưng ta có thể suy luận ra: $$E[L]=\big(E[\hat{f}(\mathbf{x})-f(\mathbf{x})]\big)^2+E[\big(\hat{f}(\mathbf{x})-E[\hat{f}(\mathbf{x})]\big)^2]+\sigma^2$$

Như vậy, kỳ vọng lỗi này có thể phân tích ra phương sai và độ lệch như sau: $$E[L]=\text{Bias}^2+\text{Var}+\text{Noise}$$ Trong đó:

• Độ lệch $\text{Bias}=E[y(\mathbf{x})-f(\mathbf{x})]$
• Phương sai $\text{Var}=E[y(\mathbf{x})^2]-E[y(\mathbf{x})]^2$
• Nhiễu $\text{Noise}=\sigma^2$

Do $\sigma^2$ được cố định từ trước bằng giả thuyết phân phối chuẩn, nên kỳ vọng lỗi của ta sẽ phụ thuộc vào 2 thành phần là độ lệch và phương sai. Từ đây ta có thể hiểu phương sai và độ lệch như sau:

• Độ lệch: Độ lệch giữa trung bình của mô hình ước lượng được và trung bình thực tế của dữ liệu. Độ lệch càng lớn thì mô hình và giá trị thực của ta sẽ càng không khớp nhau.
• Phương sai: Độ phân tán của kết quả ước lượng được của mô hình. Phương sai càng lớn thì khả năng giá trị dự đoán sẽ dao động quanh càng mạnh dẫn tới có thể lệch xa giá trị thực tế.

2. Quan hệ phương sai và độ lệch

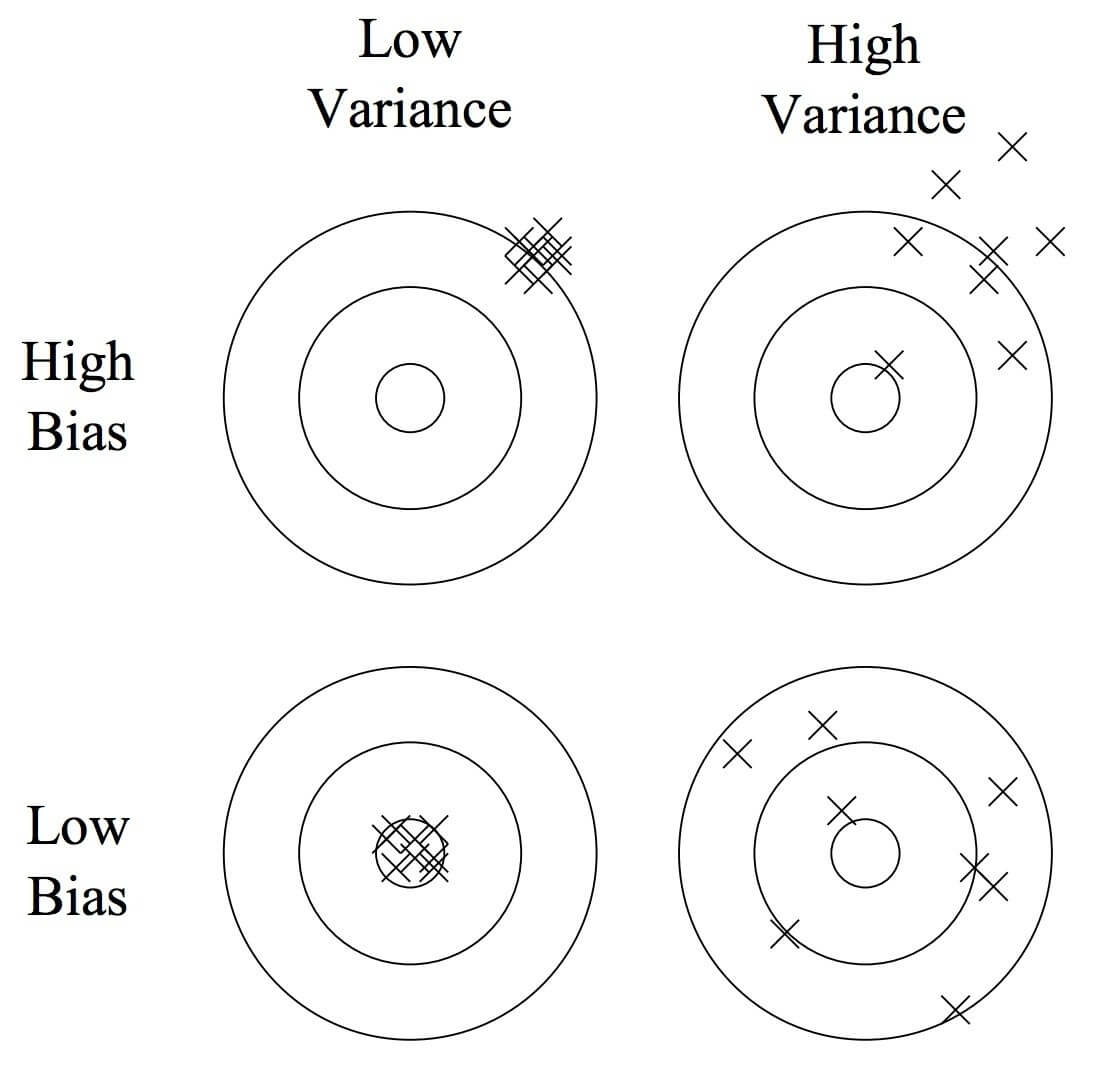
Để dễ hiểu ta có thể biểu diễn quan hệ giữa phương sai và độ lệch bằng hình vẽ dưới đây:

Hình 1: Mô tả quan hệ bias-variance. Source: https://goo.gl/g8FWko

Lý tưởng nhất là ta đạt được cả độ lệch nhỏ và phương sai bé, nhưng trong thực tế điều đó lại rất khó khăn do tập dữ liệu của ta khó mà đại diện được hết cho tất cả các khả năng.

Một mô hình mà đạt được độ lệch nhỏ và phương sai lớn thì có thể sẽ rất linh hoạt khi dự đoán nhưng kết quả dự đoán cũng bị phân tán rất mạnh dẫn tới có thể đưa ra kết quả không mong muốn. Còn mô hình mà có độ lệch lớn thì khó mà khớp được với kết quả thực tế.

Nên thường trong thực tế người ta mong muốn đâu đó cân bằng được giữa độ lệch và phương sai. Mô hình mà đạt được độ lệch không quá lớn thì kết quả có khả năng lệch ít hơn và phương sai không quá lớn giúp cho phạm vi dự đoán hẹp lại thành ra kết quả gần với mong đợi hơn.

3. Tương quan với lỗi mô hình

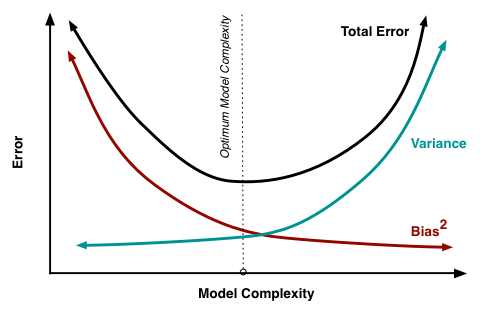
Khi huấn luyện mô hình ta sẽ thu được kết quả giữa độ phức tạp mô hình và phương sai, độ lệch như sau:

Hình 2: Tương quan với lỗi. Source: http://scott.fortmann-roe.com/docs/BiasVariance.html

Mô hình càng phức tạp thì độ lệch sẽ càng thấp đi nhưng phương sai sẽ tăng lên. Khi độ phức tạp mô hình càng tăng thì đồng nghĩa với việc mô hình càng khớp với mẫu huấn luyện thành ra độ lệch sẽ giảm đi. Mặt khác do phải khít dữ liệu nên phương sai phải rộng ra để có thể bao phủ được hết.

Chính điểm này sẽ làm cho mô hình có thể bị quá khớp với dữ liệu mẫu mà mất đi tính tổng quát khi mà phương sai lớn quá. Còn mô hình sẽ chưa khớp nếu độ lệch lớn quá. Như hình trên mô phỏng thì đâu đó điểm tối ưu sẽ là điểm cân bằng giữa phương sai và độ lệch. Đây chính là mấu chốt để có thể đoán được mô hình của ta đang ở trong trạng thái nào như bài viết trước đã phân tích.

4. Kết luận

Kỳ vọng lỗi có thể được phân tích thành phương sai và độ lệch: $$E[L]=\text{Bias}^2+\text{Var}+\text{Noise}$$

Độ lệch $\text{Bias}$ là mức độ chênh lệch giữa trung bình của mô hình và dữ liệu thực tế, còn phương sai $\text{Var}$ thể hiện độ dao động của mô hình khi dự đoán. Trên thực tế ta mong muốn tối ưu được kỳ vọng lỗi với sự cân bằng giữa độ lệch và phương sai (Bias-Variance Trade-off).

Khi mà phương sai lớn (Hight Variance) mô hình của ta sẽ bị quá khớp (Overfitting), còn độ lệch lớn (Hight Bias) thì mô hình của ta sẽ bị chưa khớp (Underfitting). Dựa vào sự biến thiên của phương sai và độ lệch chuẩn ta có được độ biến thiên của lỗi. Tại nơi mà đồ thị của lỗi đổi chiều ta sẽ có được điểm tối ưu cho mô hình. Cụ thể ra sao bạn có thể xem lại bài viết trước.