Mặc dù sử dụng công thức chuẩn để tìm tham số là có thể thực hiện được, nhưng với tập dữ liệu lớn nhiều chiều trong thực tế thì với máy tính lại không thể thực hiện được do các ràng buộc của bộ nhớ cũng như khả năng tính toán. Chưa kể với nhiều bài toán việc giải được đạo hàm để tìm ra công thức chuẩn là rất khó khăn. Nên trong thực tế giải thuật thay thế là Gradient Descent thường được sử dụng.

Chính vì vậy tôi viết bài này để hiểu rõ hơn về phương pháp tối ưu bằng giải thuật Gradient Descent cũng như các biến thể và tối ưu cho giải thuật này. Để cho thuận tiện từ giờ trở đi tôi sẽ viết tắt Gradient Descent là GD.

Mục lục

1. Gradient Descent là gì

Như trong bài đạo hàm của hàm nhiều biến đã giải thích về gradient và sự biến thiên của hàm số thì hàm số sẽ tăng nhanh nhất theo hướng của gradient (gradient ascent) và giảm nhanh nhất theo hướng ngược của gradient (gradient descent).

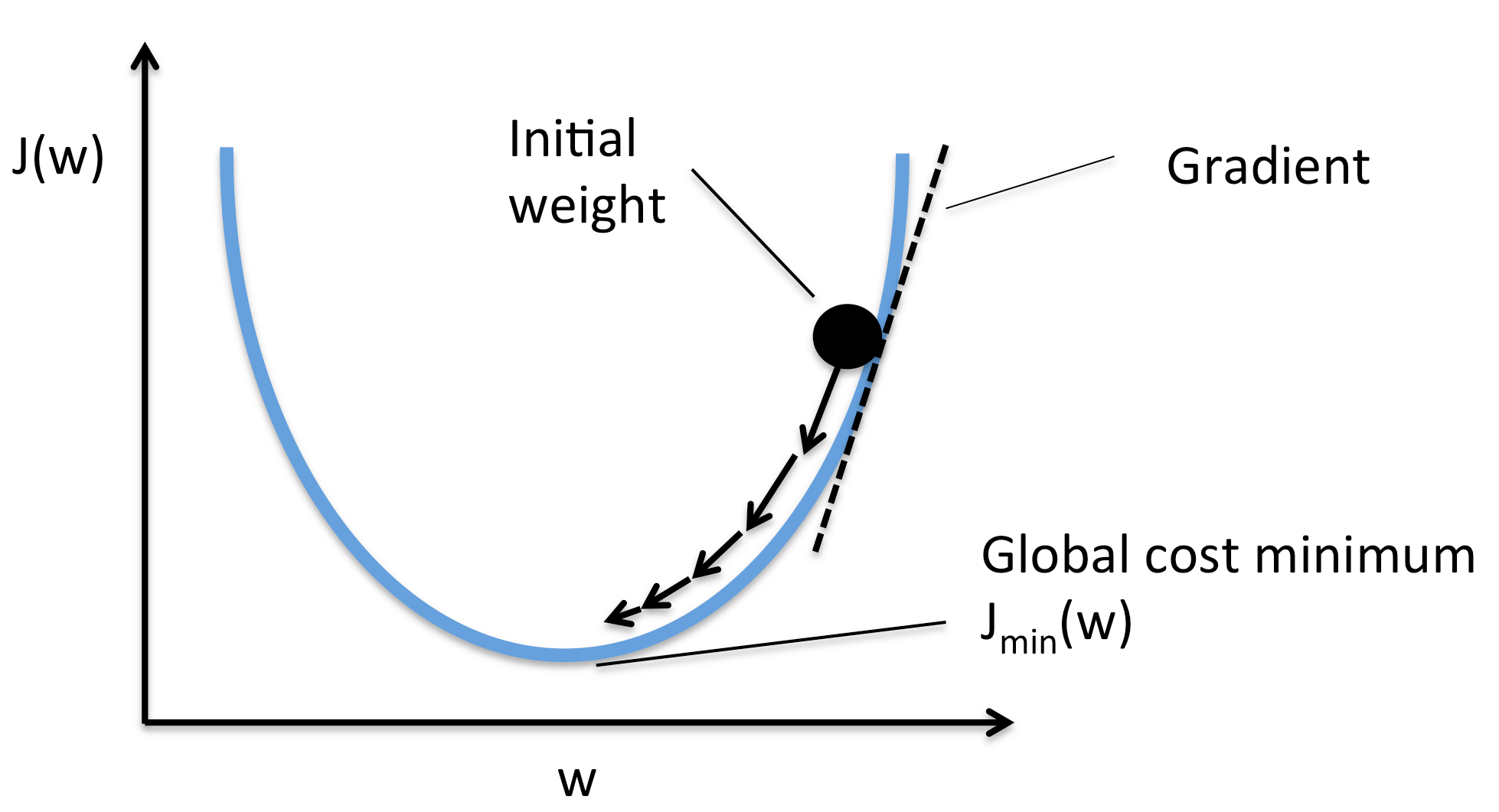
Như vậy một cách trực quan ta có thể nhận xét rằng nếu ta cứ đi ngược hướng đạo hàm mãi thì ta sẽ tới được điểm cực tiểu của hàm số. Việc này cũng tương tự như đặt một viên bi trên 1 dốc nào đó thì nó sẽ lăn xuống dốc theo hướng nghiêng của dốc. Nếu bạn cần ví dụ minh họa trực quan thì tôi nghĩ nên xem bài viết này của anh Tiệp. Theo như tôi thấy thì bài viết của anh ấy rất rõ ràng và đẩy đủ, nên tôi sẽ không phí công viết lại ở đây nữa mà sẽ tập trung vào khai triển cho lập trình.

Hình 1: Mô phỏng giải thuật Hình 1: Mô phỏng giải thuật

Giả sử ta cần tìm tham số $\theta\in\mathbb{R}^n$ để tối thiểu hoá hàm lỗi $J(\theta)$. Đầu tiên ta sẽ đặt $\theta$ tại một điểm bất kì nào đó. Sau đó giải thuật GD được thực hiện bằng cách cập nhập dần các tham số $\theta$ ngược với hướng của gradient $\nabla_\theta J(\theta)$ tại điểm hiện tại cho tới khi nó hội tụ về điểm nhỏ nhất. Tại mỗi bước cập nhập, ta sẽ dịch tham số bằng một lượng $\eta\nabla_\theta J(\theta)$ với độ học (learning rate) $\eta>0$ thể hiện cho việc dịch chuyển nhiều tới đâu: $$\theta^{(k+1)}=\theta^{(k)}-\eta\nabla_\theta J(\theta^{(k)})$$

$\theta^{(k)}$ ở đây kí hiệu cho tham số tại bước cập nhập lần $k$ khi thực hiện giải thuật GD.

Ví dụ, ta có hàm $J(\theta) = \theta_0^2+sin(\theta_1)$. Gradient (ma trận Jacobi) lúc này sẽ là: $$ \nabla_\theta J(\theta)= \begin{bmatrix} \dfrac{\partial}{\partial\theta_0}J\cr \dfrac{\partial}{\partial\theta_1}J \end{bmatrix}= \begin{bmatrix} 2\theta_0\cr \cos(\theta_1) \end{bmatrix} $$

Tại bước bất kì các tham số được cập nhập như sau: $$ \begin{cases} \theta_0=\theta_0-\eta2\theta_0 \cr \theta_1=\theta_1-\eta\cos(\theta_1) \end{cases} $$

Lưu ý rằng ta phải cập nhập đồng thời tham số sau khi tính đạo hàm chứ không được đồng thời vừa tính đạo hàm vừa cập nhập tham số. Ví dụ với Python:

gradient_descent.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
'''
Evaluate Gradient for J = theta_0^2 + sin(theta_1)
'''
def eval_grad(theta):
  # init gradient
  grad = np.empty_like(theta)
  # eval gradient
  grad[0] = 2 * theta[0]
  grad[1] = np.cos(theta[1])
  return grad

# run 1000 times
NUM_INTERS = 1000
# learning rate
ETA = 0.01

# init theta
theta = np.zeros(2)

# run GD
for (i in range(NUM_INTERS)):
  grad = eval_grad(theta)
  theta -= ETA * grad

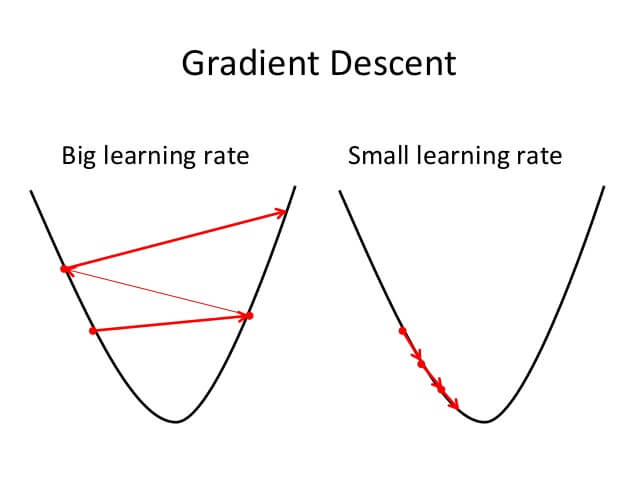
Việc chọn $\eta$ có ý nghĩa rất lớn trong phương pháp này vì nó quyết định tới tính sống còn của giải thuật. Nếu $\eta$ quá lớn thì ta không hội tụ được về đích, nhưng nếu $\eta$ quá nhỏ thì ta lại mất rất nhiều thời gian để chạy giải thuật này.

Hình 2: Ảnh hưởng của độ học η Hình 2: Ảnh hưởng của độ học η

Ngoài ra nếu để ý thì thấy nếu hàm lỗi $J(\theta)$ mà không lồi thì ta rất dễ bị rơi vào điểm tối thiểu cục bộ (local minimum) thay vì tiến được tới điểm tối thiểu toàn cục (global minimum). Việc chọn $\eta$ lúc này có vai trò rất lớn vì nếu $\eta$ hợp lý thì ta có vể vượt qua được điểm tối ưu cục bộ để tiến tiếp tới điểm tối ưu toán cục.

Thật khó để đưa ra một lời khuyên nào cho việc chọn $\eta$ vì nó còn phụ thuộc vào dữ liệu đang làm việc ra sao nữa. Nhưng thường thì người ta cứ thử nhiều giá trị và đưa ra đánh giá để chọn lấy một giá trị phù hợp. Thường mình hay bắt đầu với $\eta=0.01$ để làm việc, lý do là gì thì cũng không rõ. hé hé

Một yếu điểm nữa khi cài đặt giải thuật này là việc tính đạo hàm rất dễ bị nhầm lẫn, ta sẽ cùng xem xét trong phần tính đạo hàm dưới đây.

2. Ứng dụng cho hồi quy tuyến tính

Với bài toán hồi quy tuyến tính ta có công thức tính của hàm lỗi như sau: $$J(\theta)=\frac{1}{2m}\sum_{i=1}^m(\theta^{\intercal}\phi(\mathbf{x}_i)-y_i)^2$$ Lúc này ta có gradient: $$ \begin{aligned} \nabla_\theta J(\theta)&=\frac{1}{m}\sum_{i=1}^m(\theta^{\intercal}\phi(\mathbf{x}_i)-y_i)\phi(\mathbf{x}_i) \cr\ &=\frac{1}{m}\Phi^{\intercal}(\Phi\theta-y) \end{aligned} $$

Trong đó $\Phi$ là ma trận mẫu: $$\Phi= \begin{bmatrix} \phi_0(\mathbf{x}_1)&\phi_1(\mathbf{x}_1)&…&\phi_{n-1}(\mathbf{x}_1)\cr \phi_0(\mathbf{x}_2)&\phi_1(\mathbf{x}_2)&…&\phi_{n-1}(\mathbf{x}_2)\cr \vdots&\vdots&\ddots&\vdots\cr \phi_0(\mathbf{x}_m)&\phi_1(\mathbf{x}_m)&…&\phi_{n-1}(\mathbf{x}_m) \end{bmatrix} $$

Như vậy tại mỗi bước tham số được cập nhập: $$ \theta=\theta-\eta\frac{1}{m}\Phi^{\intercal}(\Phi\theta-y) $$

Code với Python:

gradient_descent.pygradient_descent.py
1
2
3
4
5
6
7
8
9
def gradient_descent(X, y, theta, eta, num_inters):
    # number of training examples
    m = y.size

    for i in range(num_inters):
        delta = np.dot(np.dot(X, theta) - y, X) / m
        theta -= eta * delta

    return theta

Mã nguồn mẫu đầy đủ bạn có thể xem tại đây nhé.

3. Tính đạo hàm

3.1. Tính đạo hàm

Để tính đạo hàm ta có 2 cách:

  • Phương pháp số học (numerical gradient): Phương pháp này sẽ lấy đạo hàm bằng cách tính như định nghĩa đạo hàm. Đạo hàm được định nghĩa là: $f^{\prime}(x)=\lim\limits_{h\rightarrow 0}\dfrac{f(x+h)-f(x)}{h}$. Nên nếu ta chọn $h$ rất bé thì có thể coi như lấy được đạo hàm gần đúng. Thường người ta lấy $h=\text{1e-5}$ để tính toán. Và trên thực tế thì khi sử dụng phương pháp này ta sẽ sử dụng đạo hàm 2 phía để tính, tức là: $f^{\prime}(x)=\dfrac{f(x+h)-f(x-h)}{2h}$. Phương pháp này khi thực hiện sẽ rất chậm nên thường người ta không sử dụng trong thực tế.

  • Phương pháp giải tích (analytic gradient): Phương pháp này sẽ sử dụng các công thức tính đạo hàm trong giải tích để thực hiện. Ví dụ như đạo hàm của $f(x)=2\sin(x)$ sẽ là $f^{\prime}(x)=2\cos(x)$. Phương pháp này thì nhanh nhưng rất dễ nhầm lẫn nếu công thức tính của ta bị sai.

3.2. Kiểm tra đạo hàm

Việc sử dụng phương pháp giải thích có thể dễ bị nhầm khi cài đặt nên thường người ta phải sử dụng cả phương pháp số học để kiểm tra xem việc tính đạo hàm là đúng hay sai. Nếu kết quả tính bằng giải tích và số học không chênh nhau nhiều thì ta có thể tự tin khẳng định việc cài đặt của ta là đúng đắn.

$$E_{f^{\prime}}=\frac{|f^{\prime}_n-f^{\prime}_a|}{\max(|f^{\prime}_n|,|f^{\prime}_a|)}<\epsilon$$

Trong đó $f^{\prime}_n$ là đạo hàm tính theo số học và $f^{\prime}_a$ là đạo hàm tính theo giải thích, còn $\epsilon$ là một số dương rất bé. Đạo hàm ở đây ám chỉ tới đạo hàm riêng đấy nhé, tức là với gradient ta phải so sánh đạo hàm riêng theo từng biến một.

Tới đây có thể bạn sẽ thắc mắc là tại sao không lấy $E_{f^{\prime}}=|f^{\prime}_n-f^{\prime}_a|$ thôi mà còn phải chia cho giá trị lớn nhất nữa. Câu trả lời là việc này giúp tránh được vấn đề khi mà đạo hàm quá nhỏ thì hiệu của chúng đương nhiên sẽ rất bé. Khi đó ta rất khó đánh giá được một cách tổng quát rằng liệu chúng có gần với nhau hay không. Tuy nhiên việc chia này có hạn chế là ta phải kiểm tra xem 1 trong 2 đạo hàm có khác 0 hay không. Nếu cả 2 bằng 0 thì ta coi như 2 đạo hàm bằng nhau $E_{f^{\prime}}=0$. Thường giá trị:

  • $E_{f^{\prime}}>\text{1e-2}$ thì thường đạo hàm bị lỗi.
  • $\text{1e-4}< E_{f^{\prime}}\le\text{1e-2}$ thì đạo hàm có thể chưa hợp lý lắm.
  • $E_{f^{\prime}}\le\text{1e-4}$ thì kết quả có thể chấp nhận được, tuy giá trị vẫn hơi cao một chút.
  • $E_{f^{\prime}}\le\text{1e-7}$ thì ta có thể yên tâm rằng kết quả đạt được là hợp lý.

Do việc tính đạo hàm theo phương pháp số học rất chậm nên thường ta chỉ kiểm tra đạo hàm tại bước cập nhập tham số đầu tiên mà thôi. Tuy nhiễn vẫn có khả năng rủi ro là tính lúc ấy không vấn đề gì nhưng chưa không đảm bảo được chắc chắn rằng việc thực hiện đạo hàm là đúng đắn. Mình đã từng ăn vụ này 1 lần rồi, nên để cho chắc thì kiểm tra ngẫu nhiên vài bước. Chấp nhận đau thương là bị chậm đi còn hơn là đi cả lò bánh!

4. Điều kiện dừng

Điều kiện dừng là điều kiệu để dừng việc cập nhập tham số lại. Nếu không có nó thì biết khi nào chương trình mới ngừng hoạt động phải không? Mà một chương trình máy tính chỉ có 2 kết cục duy nhất là dừng lại được hoặc sẽ không bao giờ dừng lại được. Nếu bạn quan tâm thì có thể đọc thêm ở đây nhé.

Thường thì người ta có các cách để thực hiện việc dùng giải thuật sau đây:

  • Giới hạn số lần cập nhập: Ta sẽ giới hạn số lần cập nhập tham số để chương trình dừng lại được. Tuy nhiên cách này có nhược điểm là không biết hàm lỗi của ta hội tụ được về đính hay chưa. Nếu mà đen thì ta bị dừng lại ở một giá trị gần với đích hoặc vừa nhảy qua đích một chút. Nếu tăng thêm 1 vài vòng thì có thể vừa tới đích. Nhưng ta lại không kiểm tra được tới đích hay chưa nên vấn đề này rất dễ xảy ra.

  • Kiểm tra giá trị hàm lỗi: So sánh giá trị của hàm lỗi sau 2 lần cập nhập liên tiếp hoặc sau một số lần cập nhập không quá lớn, nếu giá trị không khác nhau nhiều thì ta có thể coi là đã phần nào hội tụ được về đích rồi và ta sẽ dừng lại. Phương pháp này có nhược điểm là rất dễ bị dừng lại tại điểm mà đồ thị của hàm lỗi bằng phẳng. Chỗ này cực củ chuối! Ta vẫn không có cách nào để kiểm tra được điểm dừng lại là đích hay chưa. Tôi cho rằng bạn nên đọc thêm về vấn đề này tại đây.

  • Kiểm tra giá trị đạo hàm: So sánh giá trị của gradient sau 2 lần cập nhập liên tiếp hoặc sau một số lần cập nhập không quá lớn, nếu không khác biệt nhiều thì ta có thể dừng chương trình lại. Thường với BGD ta sẽ kiểm tra sau 2 lần cập nhập liên tiếp, còn SGD và MGD thì kiểm tra sau 1 số lần không quá lớn nào đó. Bạn đừng lo nếu chưa hiểu BGD, SGD và MGD là gì ngay nhé, vì ta sẽ xem ngay phần sau đây. Giải thuật này cũng có yếu điểm là tại nơi đạo hàm không khác nhau nhiều lắm thì chưa chắc là đích vì ta cũng chưa có cách nào kiểm tra được điểm hiện tại là đích hay không.

Ngoài các cách trên, ta còn có 1 phương pháp hơi thông minh một tẹo nữa là sau 2 lần cập nhập liên tiếp hoặc sau 1 số lần cập nhập đủ nhỏ, ta so sánh giá trị của hàm lỗi đối với tập huấn luyện (training set) và tập kiểm chứng (validation set), nếu 2 giá trị này càng ngày càng lệch nhau nhiều thì ta nên dừng lại và xem xét phương pháp học của ta. Vì sao lại thế thì tôi sẽ viết ở bài cân bằng hoá giữa độ lệch và phương sai sau, giờ thì bạn cứ tạm hiểu là nếu 2 giá trị đó ngày càng lệch nhau thì thuật toán học của ta đang bị khớp quá (over-fitting) nên việc tính toán tiếp cũng chẳng có tác dụng gì cả.

Hoặc có thể kiểm tra giá trị của hàm lỗi với tập kiểm chứng nếu giá trị của tập này không giảm được nhiều thì ta có thể coi rằng nó sẽ không thể giảm được nữa, lúc đó ta nên dừng chương trình lại để mất tốn thời gian.

5. Các biến thể

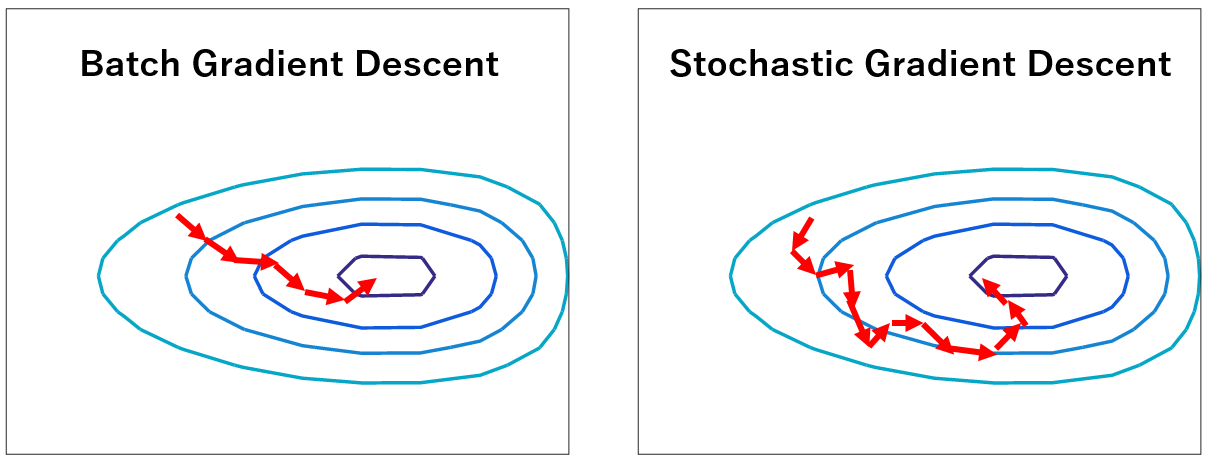
Dạng cài đặt GD từ đầu bài tới giờ được gọi là GD thuần (Vanilla GD) hay GD toàn phần (BGD - Batch GD). Đặc điểm của nó là sử dụng toàn bộ tập dữ liệu để tính đạo hàm cập nhập tham số nên có thể dẫn tới tình trạng vượt quá khả năng lưu trữ của máy tính và không thể sử dụng được cho các bài toán cần học tức thì (online training).

5.1. SGD

Thay vì sử dụng toàn bộ tập dữ liệu để cập nhập tham số thì ta có thể sử dụng từng dữ liệu một để cập nhập. Phương pháp như vậy được gọi là GD ngẫu nhiên (SGD - Stochastic Gradient Descent). Về cơ bản ở mỗi lần cập nhập tham số, ta duyệt toàn bộ các cặp mẫu $(\mathbf{x}^{(i)},y^{(i)})$ và cập nhập tương tự như BGD như sau:

$$\theta^{(k+1)}=\theta^{(k)}-\eta\nabla_\theta J(\theta^{(k)};\mathbf{x}^{(i)},y^{(i)})$$

Vì sử dụng từng mẫu đơn một nên tốc độ tính toán đạo hàm sẽ nhanh hơn rất nhiều so với BGD nhưng nó phải trả cái giá là tốc độ hội tụ bị giảm đi. Một lưu ý khi cài đặt giải thuật này là mỗi bước cập nhập ta nên xáo trộn dữ liệu rồi mới lấy ra cập nhập. Việc này giúp giảm được sự đi lòng vòng về đích của giải thuật vì ta trao khả năng cập nhập ngẫu nhiên cho nó tức là sẽ có cơ hội nhảy được 1 bước xa hơn khi tính toán.

Hình 3: So sánh BGD với SGD Hình 3: So sánh BGD với SGD

Code với Python:

stochastic_gradient_descent.py
1
2
3
4
5
6
7
8
9
10
11
def gradient_descent(X, y, theta, eta, num_inters):
    # number of training examples
    m = y.size

    for i in range(num_inters):
        np.random.shuffle(X)
        for j in X.shape[0]:
            delta = np.dot(np.dot(X[j,:], theta) - y[j], X[j,:]) / m
            theta -= eta * delta

    return theta

5.2. Mini-batch GD

Do SGD chạy chậm nên người ta thường sử dụng một phương pháp kết hợp giữa BGD và SGD là sử dụng từng nhóm dữ liệu để cập nhập tham số. Tức là ta sẽ chia dữ liệu ra thành nhiều lô khác nhau và mỗi lần cập nhập dữ liệu, thay vì sử dụng từng mẫu một ta sẽ sử dụng cả lô dữ liệu một. Phương pháp như vậy được gọi là Mini-batch GD hay viết tắt là MGD. Như vậy ta thấy rằng nếu dữ liệu ta chỉ có 1 lô thì MGD chính là BGD, nếu mỗi lô chỉ có đúng 1 mẫu thì MGD sẽ là SGD.

Giả sử lô thứ $i$ được kí hiệu là $(\mathbf{X}^{(i)},\mathbf{y}^{(i)})$, thì công thức cập nhập được viết như sau:

$$\theta^{(k+1)}=\theta^{(k)}-\eta\nabla_\theta J(\theta^{(k)};\mathbf{X}^{(i)},\mathbf{y}^{(i)})$$

Cũng như SGD ta cũng sẽ xáo trộn dữ liệu trước khi phân lô cập nhập tham số:

mini_batch_gradient_descent.py
1
2
3
4
5
6
7
8
9
10
11
def gradient_descent(X, y, theta, eta, num_inters):
    # number of training examples
    m = y.size

    for i in range(num_inters):
        np.random.shuffle(X)
        while j < X.shape[0]:
            delta = np.dot(np.dot(X[j:j+k,:], theta) - y[j:j+k], X[j:j+k,:]) / m
            theta -= eta * delta

    return theta

6. Tăng tốc GD

Để tăng tốc cho GD ta có thể sử dụng một số mẹo sau đây:

  • Song song hoá: Ta có thể thực hiện việc tính đạo hàm một cách song song bằng cách phân dữ liệu ra cho nhiều phần và sử dụng GPU hoặc nhiều máy tính kết nối với nhau để thực hiện sau đó hợp kết quả lại với nhau. Ví dụ, ta có 5 máy tính trong đó có 1 máy tính được coi là máy chủ sẽ đảm nhận việc thực hiện giải thuật còn 4 máy tính còn lại sẽ sử dụng làm phân tải tính toán. Khi đó ta chia dữ liệu làm 5 phần và phân cho mỗi máy tính thực hiện một phần dữ liệu sau đó hợp kết quả lại để tính được đạo hàm hợp. Tất nhiên là ta phải trả giá ở độ trễ mạng hay switching context nhưng nó vẫn chưa là gì so với việc tính toán hàng triệu dữ liệu với số chiều dữ liệu cũng lên tới cả triệu như vậy.

  • Chuẩn hoá đầu vào: Việc chuẩn hoá đầu vào cũng khá quan trọng, nếu dữ liệu của ta đẹp - quanh đều quanh tâm đích thì việc hội tụi về sẽ nhanh hơn ở bất kì điểm nào. Nó như việc ta bóp tròn lại một đồ thị hình eclipse. Nếu là tròn thì tại bất kì điểm nào ta cũng có thể hội tụ về đích như nhau, nhưng nếu hình eclipse thì chịu. Việc chuẩn hoá này ta có thể thực hiện bằng cái hàm $\phi(\mathbf{x})$ chẳng hạn. Tôi sẽ đi vào phần này ở các bài viết sau nên tới đây bạn cứ tạm hiểu như vậy đã ha.

7. Kết luận

Giải thuật GD - Gradient Descent hay còn gọi là BGD là một phương pháp tối ưu dựa trên gradient của hàm số. Giải thuật này sẽ cập nhập các tham số bằng cách đi ngược với gradient cho tới khi hội tụ. Mỗi lần cập nhập, ta cập nhập tham số bằng một lượng $\eta\nabla_\theta J(\theta)$: $$\theta^{(k+1)}=\theta^{(k)}-\eta\nabla_\theta J(\theta^{(k)})$$

2 biến thể khác của BGD rất hay được sử dụng là SGD - Stochastic Gradient Descent - sử dụng từng mẫu một để cập nhập: $$\theta^{(k+1)}=\theta^{(k)}-\eta\nabla_\theta J(\theta^{(k)};\mathbf{x}^{(i)},y^{(i)})$$ và MGD - Mini-batch Gradient Descent - sử dụng từng lô dữ liệu một để cập nhập: $$\theta^{(k+1)}=\theta^{(k)}-\eta\nabla_\theta J(\theta^{(k)};\mathbf{X}^{(i)},\mathbf{y}^{(i)})$$

Việc kiểm tra điều kiện dừng cho giải thuật này là rất quan trọng và gần như là việc bắt buộc khi thực hiện thuật toán. Tuỳ vào bài toán và dữ liệu bạn còn mà có thể chọn lấy 1 cách hoặc kết hợp nhiều phương pháp khác nhau để kiểm tra điều kiện dừng. Tôi thì hay kết hợp việc giới hạn số vòng và kiểm tra sự biến thiên của đạo hàm. Đôi lúc thêm cả việc kiểm tra sự biến thiên của hàm lỗi với tập kiểm chứng nữa để có thể thoát sớm.

Ngoài các phương pháp tăng tốc giải thuật đã đề cập ra thì còn nhiều giải thuật cải tiến GD nữa mà tôi sẽ viết trong một bài khác. Còn giờ nếu bạn có góp ý gì xin hãy để lại lời nhắn bên dưới nhé.