Trong các phần trước ta đã tìm hiểu về phương pháp hồi quy tuyến tính để dự đoán đầu ra liên tục, phần này ta sẽ tìm hiểu thêm một thuật toán nữa trong học có giám sát là hồi quy logistic (Logistic Regression) nhằm mục đính phân loại dữ liệu.

Mục lục

1. Định nghĩa

Phương pháp hồi quy logistic là một mô hình hồi quy nhằm dự đoán giá trị đầu ra rời rạc (discrete target variable) $y$ ứng với một véc-tơ đầu vào $\mathbf{x}$. Việc này tương đương với chuyện phân loại các đầu vào $\mathbf{x}$ vào các nhóm $y$ tương ứng.

Ví dụ, xem một bức ảnh có chứa một con mèo hay không. Thì ở đây ta coi đầu ra $y=1$ nếu bước ảnh có một con mèo và $y=0$ nếu bức ảnh không có con mèo nào. Đầu vào $\mathbf{x}$ ở đây sẽ là các pixel một bức ảnh đầu vào.

Classification with 2 groups

Để đơn giản, trước tiên ta sẽ cùng đi tìm hiểu mô hình và cách giải quyết cho bài toán phân loại nhị phân tức là $y=\{0,1\}$. Sau đó ta mở rộng cho trường hợp nhiều nhóm sau.

2. Mô hình

Sử dụng phương pháp thống kê ta có thể coi rằng khả năng một đầu vào $\mathbf{x}$ nằm vào một nhóm $y_0$ là xác suất nhóm $y_0$ khi biết $\mathbf{x}$: $p(y_0|\mathbf{x})$. Dựa vào công thức xác xuất hậu nghiệm ta có:

$$ \begin{aligned} p(y_0|\mathbf{x}) &= \dfrac{p(\mathbf{x}|y_0)p(y_0)}{p(\mathbf{x})} \cr\ &= \dfrac{p(\mathbf{x}|y_0)p(y_0)}{p(\mathbf{x}|y_0)p(y_0) + p(\mathbf{x}|y_1)p(y_1)} \end{aligned} $$

Đặt: $$a=\ln\dfrac{p(\mathbf{x}|y_0)p(y_0)}{p(\mathbf{x}|y_1)p(y_1)}$$

Ta có: $$p(y_0|\mathbf{x})=\dfrac{1}{1+\exp(-a)}=\sigma(a)$$

Hàm $\sigma(a)$ ở đây được gọi là hàm sigmoid (logistic sigmoid function). Hình dạng chữ S bị chặn 2 đầu của nó rất đặt biệt ở chỗ dạng phân phối đều ra và rất mượt.

Ở đây tôi không chứng minh, nhưng vận dụng thuyết phân phối chuẩn, ta có thể chỉ ra rằng: $$a = \mathbf{w}^{\intercal}\mathbf{x} + w_0$$ Đặt: $\mathbf{x}_0=[1,…,1]$, ta có thể viết gọn lại thành: $$a = \mathbf{w}^{\intercal}\mathbf{x}$$

Công thức tính xác suất lúc này: $$p(y_0|\mathbf{x})=\dfrac{1}{1+\exp(-a)}=\sigma(\mathbf{w}^{\intercal}\mathbf{x})$$

Trong đó, $\mathbf{x}$ là thuộc tính đầu vào còn $\mathbf{w}$ là trọng số tương ứng.

Lưu ý rằng cũng như phần hồi quy tuyến tính thì $\mathbf{x}$ ở đây không nhất thiết là đầu vào thô của tập dữ liệu mà ta có thể sử dụng các hàm cơ bản $\phi(\mathbf{x})$ để tạo ra nó. Tuy nhiên, ở đây để cho gọn gàng tôi không viết $\phi(\mathbf{x})$ như lần trước nữa.

Có công thức tính được xác suất rồi thì ta có thể sử dụng một ngưỡng $\epsilon\in [0,1]$ để quyết định nhóm tương ứng. Cụ thể: $$ \begin{cases} \mathbf{x}\in y_0 &\text{if } p(y_0|\mathbf{x})\ge\epsilon \cr \mathbf{x}\in y_1 &\text{if } p(y_0|\mathbf{x})<\epsilon \end{cases} $$

Ví dụ, $\epsilon=0.7$ thì $\mathbf{x}\in y_0$ khi mà xác suất thuộc nhóm $y_0$ của nó là trên 70%, còn dưới 70% thì ta phân nó vào nhóm $y_1$.

Dựa vào phân tích ở ví dụ mẫu phần xác suất, ta cần tối thiểu hoá làm lỗi sau: $$J(\mathbf{w})=-\frac{1}{m}\sum_{i=1}^m\Big(y^{(i)}log\sigma^{(i)} + (1-y^{(i)})log(1-\sigma^{(i)})\Big)$$

Trong đó, $m$ là kích cỡ của tập dữ liệu, $y^{(i)}$ lớp tương ứng của dữ liệu thứ $i$ trong tập dữ liệu, $\sigma^{(i)}=\sigma(\mathbf{w}^{\intercal}\mathbf{x}^{(i)})$ là xác suất tương ứng khi tính với mô hình cho dữ liệu thứ $i$.

3. Ước lượng tham số

3.1. Phương pháp GD

Để tối ưu hàm $J(\mathbf{w})$ trên, ta lại sử dụng các phương pháp Gradient Descent để thực hiện. Ở đây, đạo hàm của hàm log trên có thể được tính như sau: $$ \begin{aligned} \frac{\partial J(\mathbf{w})}{\partial w_j}&=\frac{1}{m}\sum_{i=1}^m(\sigma_j^{(i)}-y_j^{(i)})\mathbf{x}_j^{(i)} \cr\ &=\frac{1}{m}\sum_{i=1}^m\big(\sigma(\mathbf{w}^{\intercal}\mathbf{x}_j^{(i)})-y_j^{(i)}\big)\mathbf{x}_j^{(i)} \cr\ &=\frac{1}{m}\mathbf{X}_j^{\intercal}\big(\mathbf{\sigma}_j-\mathbf{y}_j\big) \end{aligned} $$

Ví dụ, theo phương pháp BGD, ta sẽ cập nhập tham số sau mỗi vòng lặp như sau: $$\mathbf{w}=\mathbf{w}-\eta\frac{1}{m}\mathbf{X}^{\intercal}\big(\mathbf{\sigma}-\mathbf{y}\big)$$

3.2. Phương pháp Newton-Raphson

Phương pháp ở phía trên ta chỉ sử dụng đạo hàm bậc nhất cho phép GD quen thuộc, tuy nhiên ở bài toán này việc sử dụng đạo hàm bậc 2 đem tại tốc độ tốt hơn.

$$\mathbf{w}=\mathbf{w}-\mathbf{H}^{-1}\nabla J(\mathbf{w})$$

Trong đó, $\nabla J(\mathbf{w})$ là ma trận Jacobi của $J(\mathbf{w})$, còn $\mathbf{H}$ là ma trận Hessian của $J(\mathbf{w})$. Hay nói cách khác, $\mathbf{H}$ là ma trận Jacobi của $\nabla J(\mathbf{w})$.

Phương pháp này có tên chính thức là Newton-Raphson. Phương pháp này không chỉ sử dụng riêng cho bài toán hồi quy logistic mà còn có thể áp dụng cho cả các bài toán hồi quy tuyến tính. Tuy nhiên, việc thực hiện với hồi quy tuyến tính không thực sự phổ biến.

Ta có: $$ \begin{aligned} \nabla J(\mathbf{w})&=\frac{1}{m}\sum_{i=1}^m(\sigma^{(i)}-y^{(i)})\mathbf{x}^{(i)} \cr\ &=\frac{1}{m}\mathbf{X}^{T}\big(\mathbf{\sigma}-\mathbf{y}\big) \end{aligned} $$

Đạo hàm của hàm sigmoid: $$\frac{d\sigma}{da}=\sigma(1-\sigma)$$

Nên: $$ \begin{aligned} \mathbf{H}&=\nabla\nabla J(\mathbf{w}) \cr\ &=\frac{1}{m}\sum_{i=1}^m\mathbf{x}^{(i)}{\mathbf{x}^{(i)}}^{\intercal} \cr\ &=\frac{1}{m}\sum_{i=1}^m\mathbf{X}^{T}\mathbf{X} \end{aligned} $$

Thế vào công thức cập nhập tham số ta có tham số sau mỗi lần cập nhập là: $$\mathbf{w}=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{y}$$

Như vậy, so với cách lấy đạo hàm bậc 1 thì cách này tỏ ra đơn giản và nhanh hơn.

4. Lập trình

Dựa vào các phân tích phía trên ta thử lập trình với BGD xem sao. Trong bài viết này tôi chỉ để cập tới đoạn mã chính để thực hiện việc tối ưu, còn toàn bộ mã nguồn bạn có thể xem trên Github.

Tập dữ liệu được sử dụng ở đây là dữ liệu bài tập trong khoá học ML của giáo sư Andrew Ng.

Dataset

Giờ ta sử dụng phương pháp BGD để tối ưu hàm $J(\mathbf{w})$:

bgd.pybgd.py

# gradient descent max step
INTERATIONS = 200000
# learning rate
ALPHA = 0.001

# calc sigmoid function
def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

# calc J function
def compute_cost(X, y, theta):
    # number of training examples
    m = y.size
    # activation
    h = sigmoid(np.dot(X, theta))
    # cost
    j = - np.sum(y * np.log(h) + (1 -  y) * np.log(1 - h)) / m
    return j

# implement BGD
def gradient_descent(X, y, theta, alpha, num_inters):
    # number of training examples
    m = y.size
    jHistory = np.empty(num_inters)

    for i in range(num_inters):
        delta = np.dot(X.T, sigmoid(np.dot(X, theta))- y) / m
        theta -= alpha * delta
        jHistory[i] = compute_cost(X, y, theta)

    return theta, jHistory

# train
theta, jHistory = gradient_descent(X, y, np.zeros(X.shape[1]), ALPHA, INTERATIONS)
print(theta)
# theta: [-7.45017822  0.06550395  0.05898701]

Kết quả thu được: $$ \begin{cases} w_0=-7.45017822 \cr w_1=0.06550395 \cr w_2=0.05898701 \end{cases} $$

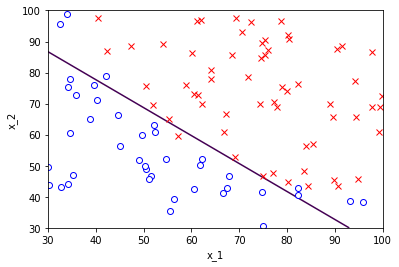
Thử vẽ đường phân tách với $\epsilon=0.5$ ta sẽ được:

Decision Boundary with ϵ=0.5

5. Phân loại nhiều nhóm

Ở phần trên ta vừa phân tích phương pháp phân loại 2 nhóm $y=\{0,1\}$, dựa vào đó ta có thể tổng quát hoá cho bài toán phân loại K nhóm $y=\{1,..,K\}$. Về cơ bản 2 có 2 phương pháp chính là:

Dựa theo phương pháp 2 nhóm
Dựa theo mô hình xác suất nhiều nhóm

Cụ thể ra sao, ta cùng xem chi tiết ngày phần dưới đây.

5.1. Dựa theo phương pháp 2 nhóm

Ta có thể sử dụng phương pháp phân loại 2 nhóm để phân loại nhiều nhóm bằng cách tính xác xuất của tầng nhóm tương ứng rồi chọn nhóm có xác suất lớn nhất là đích: $$p(y_k|\mathbf{x})=\max p(y_j|\mathbf{x})~~~,\forall j=\overline{1,K}$$

Đoạn quyết định nhóm dựa theo ngưỡng $\epsilon$ vẫn hoàn toàn tương tự như vậy. Nếu $p(y_k|\mathbf{x})\ge\epsilon$ thì $\mathbf{x}\in y_k$, còn không thì nó sẽ không thuộc nhóm $y_k$.

Phương pháp này khá đơn giản và dễ hiểu song việc thực thi có thể rất tốn kém thời gian do ta phải tính xác suất của nhiều nhóm. Bởi vậy ta cùng xem 1 giải pháp khác hiệu quả hơn như dưới đây.

5.2. Dựa theo mô hình xác suất nhiều nhóm

Tương tự như phân loại 2 nhóm, ta có thể mở rộng ra thành nhiều nhóm với cùng phương pháp sử dụng công thức xác suất hậu nghiệm để được hàm softmax sau: $$ \begin{aligned} p(y_k|\mathbf{x})=p_k&=\frac{p(\mathbf{x}|y_k)p(y_k)}{\sum_jp(\mathbf{x}|y_j)p(y_j)} \cr\ &=\frac{\exp(a_k)}{\sum_j\exp(a_j)} \end{aligned} $$

Với $a_j=\log\Big(p(\mathbf{x}|y_j)p(y_j)\Big)=\mathbf{w}_j^{\intercal}\mathbf{x}$. Trong đó, $\mathbf{w}_j$ là trọng số tương ứng với nhóm $j$, còn $\mathbf{x}$ là đầu vào dữ liệu. Tập các $\mathbf{w}_j$ sẽ được gom lại bằng một ma trận trọng số $\mathbf{W}$ với mỗi cột tương ứng với trọng số của nhóm tương ứng.

Ở đây, ta sẽ mã hoá các nhóm của ta thành một véc-to one-hot với phần tử ở chỉ số nhóm tương ứng bằng 1 và các phần tử khác bằng 0. Ví dụ: $y_1=[1,0,…,0], y_3=[0,0,1,0,…,0]$. Tập hợp các véc-tơ này lại ta sẽ có được một ma trận chéo $\mathbf{Y}$ với mỗi cột tương ứng với 1 nhóm. Ví dụ, ma trận sau biểu diễn cho tập 3 nhóm: $$ \mathbf{Y}=\begin{bmatrix} 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \end{bmatrix} $$

Như vậy, ta có thể tính xác suất hợp toàn tập với giả sử các tập dữ liệu là độc lập đôi một: $$ \begin{aligned} p(\mathbf{Y}|\mathbf{W})&=\prod_{i=1}^m\prod_{k=1}^Kp(y_k|\mathbf{x}_i)^{Y_{ik}} \cr\ &=\prod_{i=1}^m\prod_{k=1}^Kp_{ik}^{Y_{ik}} \end{aligned} $$

Trong đó, $p_{ik}=p_k(\mathbf{x}_i)$. Lấy log ta được hàm lỗi: $$J(\mathbf{W})=-\sum_{i=1}^m\sum_{k=1}^KY_{ik}\log p_{ik}$$

Như vậy, ta có thể thấy đây là công thức tổng quát của hàm lỗi trong trường hợp 2 nhóm. Công thức này còn có tên gọi là cross-entropy error function.

Việc tối ưu hàm lỗi này cũng tương tự như trường hợp 2 nhóm bằng cách lấy đạo hàm: $$\nabla_{w_j}J(\mathbf{W})=\sum_{i=1}^m\big(p_{ij}-Y_{ij}\big)\mathbf{x}_i$$

cross-entropy là cách đo độ tương tự giữ 2 phân phối xác suất với nhau. Nếu 2 phần phối càng giống nhau thì cross-entropy của chúng càng nhỏ. Như vậy để tìm mô hình gần với mô hình thực của tập dữ liệu, ta chỉ cần tối thiểu hoá cross-entropy của nó.

6. Over-fitting

Tương tự như phần hồi quy tuyến tính, ta có thể xử lý overfitting bằng phương pháp thêm hệ số chính quy hoá cho hàm lỗi: $$J(\mathbf{w})=-\frac{1}{m}\sum_{i=1}^m\Big(y^{(i)}log\sigma^{(i)} + (1-y^{(i)})log(1-\sigma^{(i)})\Big)+\lambda\frac{1}{m}\mathbf{w}^{\intercal}\mathbf{w}$$

Đạo hàm lúc này sẽ là: $$\frac{\partial J(\mathbf{w})}{\partial w_j}=\frac{1}{m}\mathbf{X}_j^{\intercal}\big(\mathbf{\sigma}_j-\mathbf{y}_j\big)+\lambda\frac{1}{m}w_j$$

7. Kết luận

Bài viết lần này đã tổng kết lại phương pháp phân loại logistic regression dựa vào cách tính xác suất của mỗi nhóm. Phương này khá đơn giản nhưng cho kết quả rất khả quan và được áp dụng rất nhiều trong cuộc sống.

Với phân loại nhị phân (2 nhóm), ta có cách tính xác suất: $$p(y_0|\mathbf{x})=\dfrac{1}{1+\exp(-a)}=\sigma(\mathbf{w}^{\intercal}\mathbf{x})$$

Hàm lỗi tương ứng: $$J(\mathbf{w})=-\frac{1}{m}\sum_{i=1}^m\Big(y^{(i)}log\sigma^{(i)} + (1-y^{(i)})log(1-\sigma^{(i)})\Big)+\lambda\frac{1}{m}\mathbf{w}^{\intercal}\mathbf{w}$$

Có đạo hàm: $$\frac{\partial J(\mathbf{w})}{\partial w_j}=\frac{1}{m}\mathbf{X}_j^{\intercal}\big(\mathbf{\sigma}_j-\mathbf{y}_j\big)+\lambda\frac{1}{m}w_j $$

Trong thực tế, ta thường xuyên phải phân loại nhiều nhóm. Việc này có thể áp dụng bằng cách lấy nhóm có xác suất lớn nhất hoặc sử dụng softmax để tính xác suất: $$p(y_k|\mathbf{x})=p_k=\frac{\exp(a_k)}{\sum_j\exp(a_j)}$$ Với $a_j=\mathbf{w}_j^{\intercal}\mathbf{x}$, trong đó véc-tơ $\mathbf{w}_j$ là trọng số tương ứng với mỗi nhóm.

[ML] Hồi quy logistic (Logistic Regression)