Lỗi ước lượng tham số có thể được chia thành 2 loại là khớp quá (over-fitting) và chưa khớp (under-fitting) với tập huấn luyện. Trong bài này sẽ nói về cách theo dõi và hạn chế các lỗi này ra sao. Trọng tâm của bài này sẽ tập trung chủ yếu vào kĩ thuật chính quy hoá (regularization) để giải quyết vấn đề khớp quá của tham số.

Mục lục

1. Giới thiệu

Mô hình của ta sau khi huấn luyện có thể đạt hiệu quả không tốt khi dự đoán với một dữ liệu mới. Chuyện này xảy ra là do mô hình của ta chưa tổng quát hoá được với toàn bộ tập dữ liệu. Nguyên nhân cũng khá dễ hiểu khi mà tập huấn luyện của ta chỉ là một tập nhỏ chưa thể đại diện cho toàn thể dữ liệu được và hơn nữa có thể nó còn bị nhiễu nữa. Người ta chia nguyên nhân ra làm 2 loại chính là chưa khớp hoặc quá khớp.

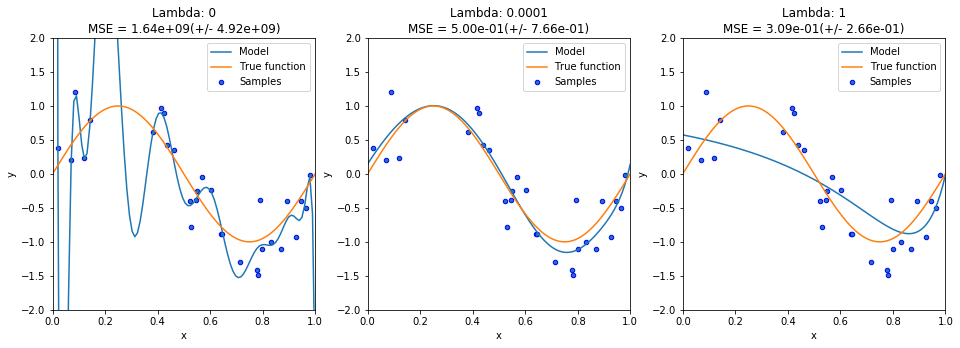
Hình 1: y=sin(2πx) model. Underfit: degree 1 (left); Goodfit: degree 3 (center); Overfit: degree 15 (right) Hình 1: y=sin(2πx) model. Underfit: degree 1 (left); Goodfit: degree 3 (center); Overfit: degree 15 (right)

1.1. Chưa khớp (Underfitting)

Mô hình được coi là chưa khớp nếu nó chưa được chưa phù hợp với tập dữ liệu huấn luyện và cả các mẫu mới khi dự đoán. Nguyên nhân có thể là do mô hình chưa đủ độ phức tạp cần thiết để bao quát được tập dữ liệu. Ví dụ như hình 1 phía bên trái ở trên. Tập dữ liệu huấn luyện loanh quanh khúc $y=sin(2\pi x)$ thế nhưng mô hình của ta chỉ là một đường thẳng mà thôi. Rõ ràng như vậy thì nó không những không thể ước lượng được giá trị của $y$ với $x$ mới mà còn không hiệu quả với cả tập dữ liệu $(x,y)$ có sẵn.

1.2. Quá khớp (Overfitting)

Mô hình rất hợp lý, rất khớp với tập huấn luyện nhưng khi đem ra dự đoán với dữ liệu mới thì lại không phù hợp. Nguyên nhân có thể do ta chưa đủ dữ liệu để đánh giá hoặc do mô hình của ta quá phức tạp. Mô hình bị quá phức tạp khi mà mô hình của ta sử dụng cả những nhiễu lớn trong tập dữ liệu để học, dấn tới mất tính tổng quát của mô hình. Ví dụ như ở hình 1 phía bên phải ở trên. Mô hình của ta gần như mong muốn bao được hết tất cả các điểm làm cho biên độ dao động của nó lớn quá mức. Mô hình này mà dự đoán với 1 giá trị mới của $x$ thì khả năng $y$ sẽ bị lệch đi rất nhiều.

1.3. Vừa khớp (Good Fitting)

Mô hình này nằm giữa 2 mô hình chưa khớp và quá khớp cho ra kết quả hợp lý với cả tập dữ liệu huấn luyện và các giá trị mới, tức là nó mang được tính tổng quát như hình 1 ở giữa phía trên. Lý tưởng nhất là khớp được với nhiều dữ liệu mẫu và cả các dữ liệu mới. Tuy nhiên trên thực tế được mô hình như vậy rất hiếm.

2. Theo dõi lỗi

Với định nghĩa như trên ta cần phương pháp để đánh giá được mô hình trước khi có thể đưa ra được biện pháp cải tiến. Trước tiên ta quy định một số thông số lỗi để phục vụ cho việc đánh giá mô hình.

2.1. Đánh giá lỗi

Ở đây ta sẽ lấy trung bình lỗi của toàn bộ tập dữ liệu để đánh giá: $$E(\theta)=\frac{1}{m}\sum_{i=1}^m err(\hat y^{(i)},y^{(i)})$$

Trong đó $E(\theta)$ là lỗi ứng với tham số $\theta$ ước lượng được của tập dữ liệu gồm có $m$ mẫu. $err(\hat y,y)$ thể hiện cho sự khác biệt giữa giá trị dự đoán $\hat y$ và giá trị thực tế $y$. Đương nhiên là nếu $\hat y=y$ thì $err(\hat y^{(i)},y^{(i)})=0$. Thường người ta lấy $err(\hat y^{(i)},y^{(i)})=\Vert \hat y^{(i)}-y^{(i)}\Vert_2^2$ giống như các hàm lỗi của mô hình. Khi đó lỗi của ta được gọi là lỗi trung bình bình phương (MSE - Mean Squared Error): $$E(\theta)=\frac{1}{m}\sum_{i=1}^m\Vert \hat y^{(i)}-y^{(i)}\Vert_2^2$$

Như đã đề cập trong phần các bước của học máy thì dữ liệu của ta sẽ được phân chia làm 3 phần là tập huấn luyện (training set) 60%, tập kiểm chứng (cross validation set) 20% và tập kiểm tra (test set) 20%. Ứng với mỗi phần ta sẽ đưa ra thông số lỗi tương ứng:

  • Tập huấn luyện: $\displaystyle E_{train}(\theta)=\frac{1}{m_{train}}\sum_{i=1}^{m_{train}}err(\hat y_{train}^{(i)},y_{train}^{(i)})$
  • Tập kiểm chứng: $\displaystyle E_{CV}(\theta)=\frac{1}{m_{CV}}\sum_{i=1}^{m_{CV}}err(\hat y_{CV}^{(i)},y_{CV}^{(i)})$
  • Tập kiểm tra: $\displaystyle E_{test}(\theta)=\frac{1}{m_{test}}\sum_{i=1}^{m_{test}}err(\hat y_{test}^{(i)},y_{test}^{(i)})$

Với mô hình hồi quy tuyến tính ta có thể lấy luôn hàm lỗi $\displaystyle J(\theta)=\frac{1}{2m}\sum_{i=1}^m(\hat y^{(i)}-y^{(i)})^2$ để đánh giá lỗi. Đương nhiên là ứng với mỗi phần dữ liệu ta phải sử dụng dữ liệu của phần tương ứng để đánh giá: $$ \begin{cases} E_{train}(\theta)=\displaystyle\frac{1}{2m_{train}}\sum_{i=1}^{m_{train}}(\hat y_{train}^{(i)}-y_{train}^{(i)})^2 \cr E_{CV}(\theta)=\displaystyle\frac{1}{2m_{CV}}\sum_{i=1}^{m_{CV}}(\hat y_{CV}^{(i)}-y_{CV}^{(i)})^2 \cr E_{test}(\theta)=\displaystyle\frac{1}{2m_{test}}\sum_{i=1}^{m_{test}}(\hat y_{test}^{(i)}-y_{test}^{(i)})^2 \end{cases} $$

2.2. Phán định lỗi

Với cách định nghĩa lỗi như trên thì một mô hình:

  • Chưa khớp: Cả $E_{train},E_{CV},E_{test}$ đều lớn.
  • Quá khớp: $E_{train}$ nhỏ còn $E_{CV},E_{test}$ lại lớn.
  • Vừa khớp: Cả $E_{train},E_{CV},E_{test}$ đều nhỏ.

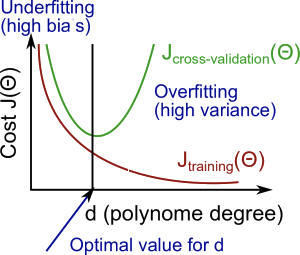
Tuy nhiên khi huấn luyện bạn không được phép sờ tới tập kiểm tra, nên ta sử dụng 2 tập huấn luyện và kiểm chứng để dự đoán kiểu lỗi. Ví dụ hình dưới đây mô tả lỗi đồ thị của $E_{train}(\theta)$ và $E_{CV}(\theta)$.

Hình 2: Đồ thị của các lỗi. Source: https://www.coursera.org/learn/machine-learning/ Hình 2: Đồ thị của các lỗi. Source: https://www.coursera.org/learn/machine-learning/

Ở hình trên ta thấy rằng, trước điểm $d$ - bậc của đa thức hợp lý thì cả 2 lỗi đều có chiều hướng giảm dần, nhưng vượt qua điểm này thì lỗi tập huấn luyện vẫn tiếp tục nhỏ đi còn tập kiểm chứng lại vọt lên. Điều đó chứng tỏ rằng phía trước $d$ ta thu được lỗi chưa khớp và sau $d$ là lỗi quá khớp, còn ở $d$ là vừa khớp.

Một cách tổng quát, ta có thể dựa vào sự biến thiên của $E_{train}$ và $E_{CV}$ như trên để có phán định về tính chất của lỗi:

  • $E_{train}$ và $E_{CV}$ đều lớn: Chưa khớp
  • $E_{train}$ và $E_{CV}$ đều nhỏ: Vừa khớp
  • $E_{train}$ nhỏ còn $E_{CV}$ lớn: Khớp quá

3. Xử lý lỗi

3.1. Điểm hợp lý

Đồ thị trên còn cho ta một gợi ý rất quan trọng là ta có thể đoán được điểm hợp lý để dừng lại khi huấn luyện. Điểm dừng ở đây chính là điểm mà đồ thị của $E_{CV}$ đổi hướng. Khi bắt đầu thấy $E_{CV}$ đổi hướng sau một số vòng lặp nào đó thì ta sẽ dừng việc huấn luyện lại và chọn lấy điểm bắt đầu có sự đổi hướng này làm điểm hợp lý cho tham số và siêu tham số. Nếu bạn cần đọc thêm về việc dừng này thì có thể đọc ở phần điều kiện dừng ở phần tối ưu hàm lỗi.

3.2. Chưa khớp

Như đã đề cập chuyện này xảy ra khi mà mô hình của ta chưa đủ phức tạp. Như vậy ta cần phải tăng độ phức tạp của mô hình lên. Để tăng độ phức tạp ta có thể lấy thêm tính năng cho mẫu bằng cách thêm các $\phi(\mathbf{x})$ khác nhau. Ví dụ, tăng bậc của đa thức lên có thể giúp ta khớp hơn với tập dữ liệu chẳng hạn. Cụ thể thì bạn có xem lại ví dụ 2 của bài về hồi quy tuyến tính.

Khi xảy ra lỗi chưa khớp thì ta cần lưu ý tới một điểm quan trọng là tăng dữ liệu không giúp mô hình tốt hơn. Tại sao lại thế thì ta sẽ cùng bàn về lý thuyết cân bằng giữa phương sai vào độ lệch ở bài viết sau.

3.3. Quá khớp

Khi xảy quá khớp ta có thể bỏ bớt tính năng đi để giảm độ phức tạp mô hình. Hoặc có thể lấy thêm dữ liệu để mô hình có thể học được một cách tổng quát hơn. Thật khó đưa ra được một cách cụ thể ngoài việc kết hợp của tất cả các kiểu xử lý trên lại với nhau sau đó đưa ra đánh giá cụ thể sau.

Ngoài ra, ta còn có một kĩ thuật nữa rất phổ biến trong học máy là chính quy hoá mà ta sẽ cùng xem xét ở phần ngay dưới đấy.

4. Kĩ thuật chính quy hoá

4.1. Định nghĩa

Chính quy hoá (regularization) là một kĩ thuật giúp giảm lỗi khớp quá bằng cách thêm một phần chính quy hoá vào hàm lỗi như sau: $$J(\theta)=E_X(\theta)+\lambda E_\theta(\theta)$$

$E_X(\theta)$ là hàm lỗi ban đầu và cụm $\lambda E_\theta(\theta)$ mới thêm vào là số hạng chính quy hoá đóng vai trò như một biện pháp phạt lỗi (penalization).

Hình 3: y=sin(2πx) L2. Without Ridge: λ=0 (left); Ridge: λ=1e-4 (center); Ridge: λ=1 (right) Hình 3: y=sin(2πx) L2. Without Ridge: λ=0 (left); Ridge: λ=1e-4 (center); Ridge: λ=1 (right)

Trong đó, hệ số chính quy hoá $\lambda$ được chọn từ trước để cân bằng giữa $E_X(\theta)$ và $E_\theta(\theta)$. $\lambda$ càng lớn thì ta càng coi trọng $E_\theta(\theta)$, ít coi trọng tham số cho hàm lỗi ban đầu hơn, dẫn tới việc các tham số $\theta$ ít có ảnh hưởng tới mô hình hơn. Hay nói cách khác là mô hình bớt phức tạp đi giúp ta đỡ việc lỗi quá khớp.

$E_\theta(\theta)$ ở đây sẽ không bao gồm độ lệch $\theta_0$ và thường có dạng như sau: $$E_\theta(\theta)=\frac{1}{p}\Vert\theta\Vert_p^p=\frac{1}{p}\sum_{i=1}^n|\theta_i|^p$$

Khi đó, hàm lỗi có thể viết lại như sau: $$J(\theta)=E_X(\theta)+\lambda\frac{1}{p}\sum_{i=1}^n|\theta_i|^p$$

$p$ thường được chọn là 2 (L2 Norm) và 1 (L1 Norm hay còn được gọi là Lasso trong thống kê).

Với L2, hàm lỗi có dạng: $$J(\theta)=E_X(\theta)+\frac{\lambda}{2}\theta^{\intercal}\theta$$

Với L1, hàm lỗi có dạng: $$J(\theta)=E_X(\theta)+\lambda\sum_{i=1}^n|\theta_i|$$

Phương pháp chính quy hoá này còn có tên là cắt trọng số (weight decay) vì nó làm cho các trọng số (tham số $\theta$) bị tiêu biến dần về 0 trong khi học. Còn trong thống kê, phương pháp này có tên là co tham số (parameter shrinkage) vì nó làm co lại các giá trị tham số dần về 0.

4.2. Công thức chuẩn

Với hàm lỗi của hồi quy tuyến tính thì ta thường chia lấy trung bình của toàn mẫu nên số hạng chính quy hoá cũng sẽ được chia tương tự. Ngoài ra ta cũng thường lấy L2 để thực hiện việc chính quy hoá, nên: $$J(\theta)=\frac{1}{2m}\sum_{i=1}^m\Big(\theta^{\intercal}\phi(\mathbf{x}_i)-y_i\Big)^2+\frac{\lambda}{2m}\theta^{\intercal}\theta$$

Khi đó, công thức chuẩn được viết lại như sau: $$\hat\theta=(\lambda\mathbf{I}+\Phi^{\intercal}\Phi)^{-1}\Phi^{\intercal}\mathbf{y}$$

4.3. Tính đạo hàm

Việc tính đạo hàm nhằm thực hiện giải thuật tối ưu với Gradient Descent.

Đạo hàm khi có số hạng chính quy hoá với:

  • L2 : $\dfrac{\partial E_X(\theta)}{\partial\theta_i}+\lambda\theta_i$
  • L1 : $\dfrac{\partial E_X(\theta)}{\partial\theta_i}+\lambda\text{sgn}(\theta_i)$

Lưu ý: đạo hàm này không tính cho $\theta_0$. Nói cách khác $\theta_0$ không được thêm số hạng chính quy hoá.

Trường hợp của bài toán hồi quy tuyến tính:

$$\frac{\partial}{\partial\theta_i}=\frac{1}{m}\sum_{j=1}^m(\theta^{\intercal}\phi(\mathbf{x}_j)-y_j)\mathbf{x_j}+\begin{cases}0 &\text{for }i=0\cr\frac{\lambda}{m}\theta_i &\text{for }i>0\end{cases}$$

Gradient có dạng sau: $$\Delta_\theta J(\theta)=\frac{1}{m}(\theta^{\intercal}\Phi-y)\Phi+\frac{\lambda}{m}\theta$$

Đương nhiên là khi tính số hạng chính quy hoá ta gắn $\theta_0\triangleq 0$ để tiêu biến số hạng đó đi.

4.4. Cài đặt

Hệ số chính quy hoá $\lambda$ thường nhỏ để không quá ảnh hưởng nhiều tới việc tối ưu lỗi truyền thống. Thường người ta sẽ chọn lấy 1 danh sách các $\lambda$ để huấn luyện và lấy một giá trị tối ưu nhất. Tuy nhiên, lưu ý rằng hệ số này không dùng cho tập kiểm chứng khi đối chiếu để đánh giá mô hình.

Cụ thể các bước cài đặt như sau:

  1. Tạo danh sách các $\lambda$.
  2. Tạo các mô hình tương ứng với các $\phi(\mathbf{x})$ tương ứng. Ví dụ như bậc của đa thức hay co giãn các thuộc tính chẳng hạn.
  3. Học tham số $\theta$ ứng với từng $\lambda$ một.
  4. Tính lỗi với tập kiểm chứng $E_{CV}(\theta)$ ứng với tham số $\theta$ học được (lúc này đặt $\lambda=0$).
  5. Chọn lấy mô hình ứng với tham số và $\lambda$ cho ít lỗi nhất với tập kiểm chứng.
  6. Lấy $\theta$ và $\lambda$ tương ứng rồi tính lỗi cho tập kiểm tra $E_{test}(\theta)$ và đánh giá mô hình.

Nếu hứng thú bạn có thể xem ví dụ cài đặt thuật toán với chính quy hoá tại đây nhé.

5. Kết luận

Đánh giá mô hình có thể chia thành 3 dạng chưa khớp khi nó chưa đủ độ phức tạp, quá khớp khi nó quá phức tạp và vừa khớp khi mà nó vừa đủ để tổng quát hoá. Khi huấn luyện ta có thể sử dụng tập huấn luyện và tập kiểm chứng để đánh giá mô hình đang ở tình trạng nào. Nếu $E_{train},E_{CV}$ đều lớn thì ta nói rằng nó chưa khớp, còn $E_{train}$ nhỏ và $E_{CV}$ lớn thì ta nói rằng nó bị quá khớp.

Bài toán chưa khớp thì ta có thể giải quyết bằng cách phức tạp hoá mô hình lên còn với bài toán quá khớp thì ta có thể sử dụng phương pháp chính quy hoá để giải quyết: $$J(\theta)=E_X(\theta)+\lambda E_\theta(\theta)$$

Hệ số $\lambda$ càng lớn thì mô hình sẽ càng đơn giản đi từ đó giúp tránh được chuyện quá khớp nhưng cũng dẫn tới việc chưa khớp. Nên ta cần phải chọn được giá trị $\lambda$ hợp lý. Thường ta sẽ đưa ra 1 danh sách các hệ số $\lambda$ rồi chạy lần lượt và chọn lấy một giá trị tốt nhất. Tuy nhiên ta cần phải nhớ rằng cụm chuẩn hoá này không dùng cho tập kiểm chứng khi huấn luyện.

Mặc dù qua bài này còn đôi chỗ hơi khó hiểu và mơ hồ nhưng nhìn chung nếu chỉ lập trình thì ta nhớ lấy hệ số $\lambda$ là được. Nếu bạn hứng thú tìm hiểu tận gốc vấn đề thì ta sẽ cùng xem trong bài viết tới về vấn đề cân bằng giữa phương sai và độ lệch của mô hình.