Phương pháp nhân tử Lagrange (method of Lagrange multipliers) là một kỹ thuật cực kì hữu dụng để giải các bài toán tối ưu có ràng buộc. Trong chuỗi bài viết này tối sẽ chia làm 2 phần: (1) Ràng buộc là đẳng thức; (2) Ràng buộc là bất đẳng thức. Bài viết đầu tiên này tôi sẽ tập trung vào tối ưu có ràng buộc là đẳng thức.

Mục lục

1. Kỹ thuật Lagrange

1.1. Phát biểu bài toán

Tìm cực trị của hàm số đa biến $\color{#0c7f99}f(\mathbf{x})$ thoả mãn điều kiện hàm đa biến $\color{#bc2612}g(\mathbf{x})=c$ với $c$ là hằng số: $$ \begin{aligned} \text{maximize (or minimize)}&\color{#0c7f99}f(\mathbf{x}) \cr\text{subject to:}~&\color{#bc2612}g(\mathbf{x}) = c \end{aligned} $$

1.2. Ứng dụng kỹ thuật nhân tử Lagrange

Để giải quyết bài toàn này, ta sử dụng kỹ thuật Lagrange như sau:

• Bước 1: Thêm một biến nhân tử Lagrange $\color{#0d923f}\lambda$ và định nghĩa một hàm Lagrangian $\mathcal{L}$ như sau: $$\mathcal{L}(\mathbf{x},\textcolor{#0d923f}\lambda)=\textcolor{#0c7f99}{f(\mathbf{x})}-\textcolor{#0d923f}\lambda\big(\textcolor{#bc2612}{g(\mathbf{x})-c}\big)$$
• Bước 2: Giải đạo hàm (gradient) của $\mathcal{L}$ bằng véc-to $\mathbf{0}$: $$\nabla\mathcal{L}(\mathbf{x},\textcolor{#0d923f}\lambda)=\mathbf{0}$$
• Bước 3: Dựa vào các nghiệm $(\mathbf{x^* },\textcolor{#0d923f}\lambda^* )$ tìm được ở trên, thế vào hàm $\color{#0c7f99}f(\mathbf{x})$ rồi chọn giá trị lớn nhất (nhỏ nhất) là ta được giá trị cần tìm (thực ra chỉ cần nghiệm $\mathbf{x^* }$ là đủ): $$ \begin{cases} \textcolor{blue}{f_{min}} &= \displaystyle\min_{\mathbf{x^* }}\color{#0c7f99}f(\mathbf{x^* }) \cr \textcolor{red}{f_{max}} &= \displaystyle\max_{\mathbf{x^* }}\color{#0c7f99}f(\mathbf{x^* }) \end{cases} $$

Nếu bạn để ý một chút thì phương trình ở bước 2 tương đương với hệ phương trình sau: $$ \begin{cases} \nabla\textcolor{#0c7f99}{f(\mathbf{x})} &= \textcolor{#0d923f}\lambda\nabla\textcolor{#bc2612}{g(\mathbf{x})} \cr \color{#bc2612}g(\mathbf{x}) &= \color{#bc2612}c \end{cases} $$

Bởi: $$ \nabla\mathcal{L}(\mathbf{x},\textcolor{#0d923f}\lambda)= \begin{bmatrix} \dfrac{\partial\mathcal{L}}{\partial\mathbf{x}} \cr\cr \dfrac{\partial\mathcal{L}}{\partial\mathbf{\textcolor{#0d923f}\lambda}} \end{bmatrix}= \begin{bmatrix} \nabla\textcolor{#0c7f99}{f(\mathbf{x})}-\textcolor{#0d923f}\lambda\nabla\textcolor{#bc2612}{g(\mathbf{x})} \cr \color{#bc2612}g(\mathbf{x})-c \end{bmatrix} $$

Tức là ở đây, khi giải bằng tay bạn có thể làm ngơ hàm $\mathcal{L}(\mathbf{x},\textcolor{#0d923f}\lambda)$ mà vẫn giải tốt. Tuy nhiên, việc biểu diễn qua hàm Lagrangian này sẽ giúp ta dễ dàng sài luôn được các cách giải phổng thông khác và các chương trình máy tính có sẵn.

1.3. Ví dụ minh họa

Bài toán:
Giả sử nhà máy của bạn sản suất thiết bị phụ tùng bằng thép. Chi phí nhân công mỗi giờ là $\$20$ và giá 1 tấn thép là $\$170$. Lợi nhuận $R$ được mô hình hoá như sau:

$$R(h,s)=200h^{{2}/{3}}s^{{1}/{3}}$$ Trong đó:

• $h$ là số giờ làm việc
• $s$ là số tấn thép

Hãy tính lợi nhuận lớn nhất có thể thu được nếu kinh phí của bạn là $\$20,000$.

Lời giải:
Mỗi giờ làm việc tốn $\$20$ và mỗi tấn thép tốn $\$170$ nên tổng chi phí tính theo $h$ và $s$ là: $$B(h,s)=20h+170s$$ Do kinh phí $B$ là $\$20,000$ nên ta có ràng buộc: $$\color{#bc2612}20h+170s=20,000$$

Để có cái nhìn rõ ràng hơn về bài toán, ta thử biểu diễn nó qua đồ thị như sau:

Đồ thị lợi nhuận và ràng buộc. Source: khanacademy

Nhìn vào đồ thị trên ta có thể thấy lợi nhuận (đường màu xanh) đạt lớn nhất với điều kiện ngân quỹ (đường màu đỏ) tại điểm giao bên trái của 2 đường.

Cái nhìn trực quan là thế, còn giờ ta sẽ giải bằng phương pháp nhân tử Lagrange để tối ưu hoá hàm $\color{#0c7f99}R(h,s)$ ràng buộc bởi đẳng thức $\color{#bc2612}{B(h,s)}=20,000$. Theo phân tích ở trên ta sẽ có: $$ \begin{cases} \nabla\textcolor{#0c7f99}{R(h,s)} &= \textcolor{#0d923f}\lambda\nabla\textcolor{#bc2612}{B(h,s)} \cr \color{#bc2612}B(h,s) &= \color{#bc2612}20,000 \end{cases} $$

Phân tích ra ta được: $$ \begin{cases} \color{#0c7f99}200\cdot\dfrac{2}{3}h^{-{1}/{3}}s^{{1}/{3}} &= 20\textcolor{#0d923f}\lambda \cr\cr \color{#0c7f99}200\cdot\dfrac{1}{3}h^{{2}/{3}}s^{-{2}/{3}} &= 170\textcolor{#0d923f}\lambda \cr\cr \color{#bc2612}20h+170s &= \color{#bc2612}20,000 \end{cases} $$

Giải ra ta có kết quả: $$ \begin{cases} \textcolor{#0c7f99}h &= \dfrac{2,000}{3} \approx 667 \cr\cr \textcolor{#0c7f99}s &= \dfrac{2,000}{51} \approx 39 \cr\cr \color{#0d923f}\lambda &= \sqrt[3]{\dfrac{8,000}{459}} \approx 2.593 \end{cases} $$

Thế vào công thức tính lợi nhuận ta có: $$R(667, 39)=200(667)^{{2}/{3}}(39)^{{1}/{3}} \approx \fcolorbox{red}{aqua}{51,777}$$

Như vậy, để đạt được lợi nhuận lớn nhất ta cần 667 giờ lao động với 39 tấn thép và lợi nhận có thể đạt được tối đa là $\$51,777$.

2. Phân tích Lý thuyết

2.1. Cái nhìn hình học

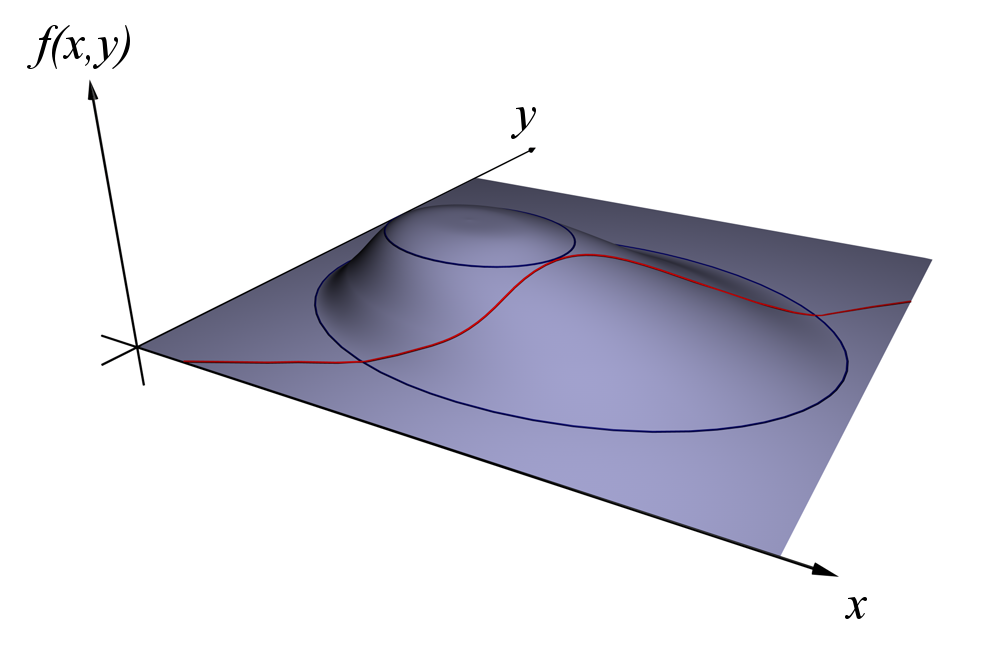
Chiếu đồ hình của $\color{#0c7f99}f(\mathbf{x})$ và $\color{#bc2612}g(\mathbf{x})=c$ qua dạng đường đồng mức (Contour Line). Đầu tiên ta có thể thấy rằng giá trị cực trị của hàm $\color{#0c7f99}f(\mathbf{x})$ bị ràng buộc bởi $\color{#bc2612}g(\mathbf{x})=c$ chính là điểm tiếp xúc của đường đồng mức của chúng.

Đường đồng mức của $f(x,y)$ là tập của tất cả các điểm $(x^* ,y^* )$ để $f(x^* ,y^* )=k$ với $k$ là hằng số.

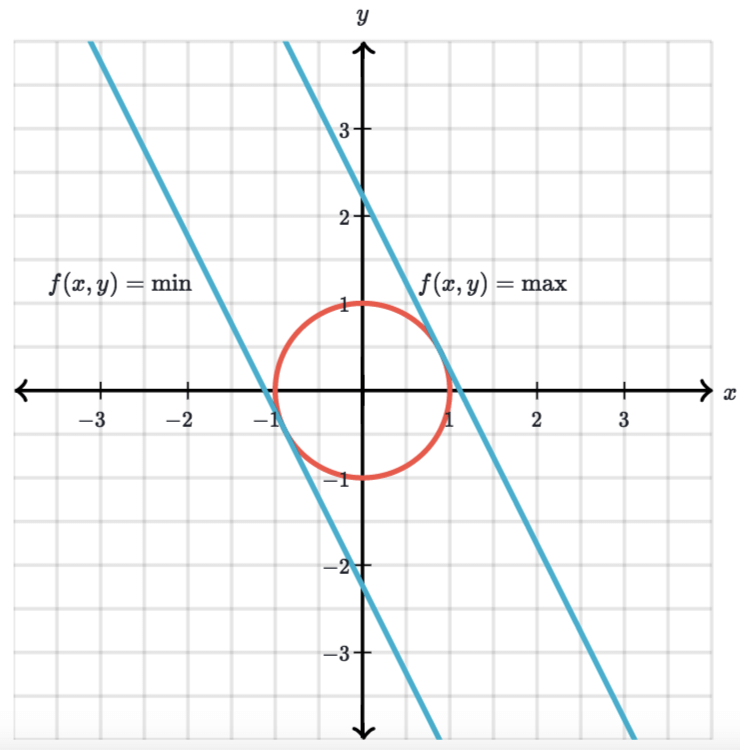
Ví dụ, với $\color{#0c7f99}f(\mathbf{x})=2x+y$, $\color{#bc2612}g(\mathbf{x})=x^2+y^2$ và $\color{#bc2612}c=1$, ta sẽ có mô hình đồ thị như sau.

Đồ thị của f(x,y) và g(x,y). Source: khanacademy

Đường đồng mức khi được chiếu xuống sẽ có dạng:

Đường đồng mức của f(x,y) và g(x,y). Source: khanacademy

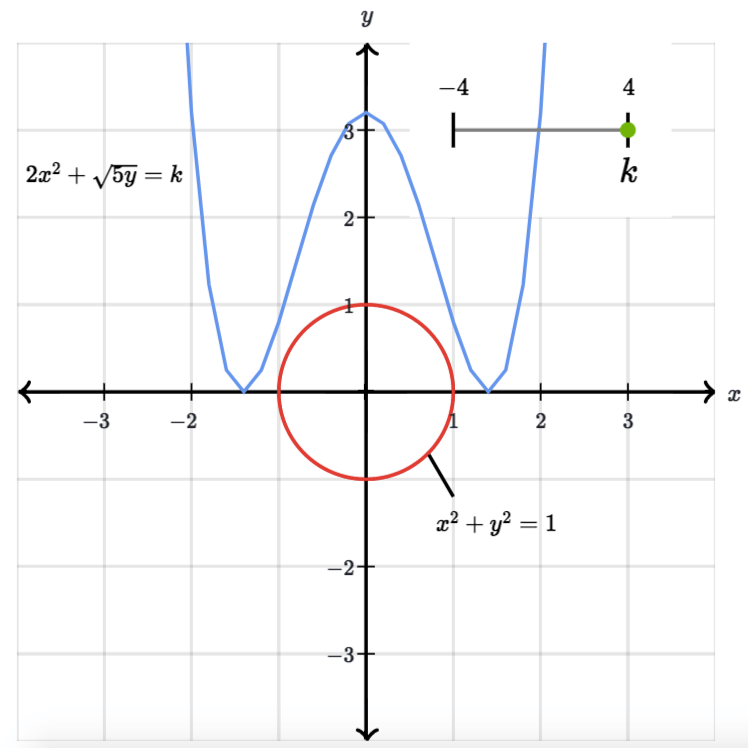
Nhìn vào biểu đồ trên ta có thể thấy 2 điểm cực trị là điểm tiếp xúc của 2 đường đồng mức của 2 hàm mục tiêu và ràng buộc. Tuy nhiên, không phải lúc nào $\color{#0c7f99}f(\mathbf{x})$ cũng thẳng tưng thế nhé, vì nó còn phụ thuộc vào dạng của hàm đó là gì. Ví dụ $\color{#0c7f99}f(\mathbf{x})=2x^2+\sqrt{5y}$ thì đường đồng mức sẽ là:

Đường đồng mức của f(x,y) và g(x,y). Source: khanacademy

Nhưng dù thế nào đi nữa, nếu $k$ là điểm cực trị của hàm $\color{#0c7f99}f$ thì đường đồng mức $\color{#0c7f99}f(x,y)=k$ sẽ luôn tiếp xúc với đường đồng mức của $\color{#bc2612}g(\mathbf{x})=c$ tại điểm đó.

Mặt khác, gradient lại luôn vuông góc với đường đồng mức tại điểm tương ứng.

Gradient vuông góc với đường đồng mức. Source: khanacademy

Như vậy, nếu 2 đường đồng mức tiếp xúc nhau thì gradient tương ứng của chúng tại điểm tiếp xúc là song song với nhau.

Gradient tại điểm tiếp xúc. Source: khanacademy

Nói cách khác, giả sử điểm tiếp xúc đó là $(x_0,y_0)$ thì ta có thể biểu diễn quan hệ gradient của chúng như sau: $$\nabla\textcolor{#0c7f99}{f(x_0,y_0)}=\textcolor{#0d923f}{\lambda_0}\nabla\textcolor{#bc2612}{g(x_0,y_0)}$$

Trong đó $\textcolor{#0d923f}\lambda$ là một hằng số nào đó. Qua phép biểu diễn này ta có thể quy được thành một hệ phương trình 3 ẩn 3 phương trình và hoàn toàn có thể giải được rất dễ dàng: $$ \begin{cases} \color{#bc2612}g(x,y) = c \cr \nabla\textcolor{#0c7f99}{f(x,y)}=\textcolor{#0d923f}{\lambda}\nabla\textcolor{#bc2612}{g(x,y)} \end{cases} $$

Nghiệm của hệ phương trình trên $(x_0,y_0,\textcolor{#0d923f}{\lambda_0})$ khi thay thế lại hàm $\color{#0c7f99}f(x,y)$ sẽ cho ta được kết quả mong muốn.

2.2. Gom lại thành 1 hàm

Từ hệ phương trình trên, Lagrange gom lại thành một phương trình Lagrangian duy nhất: $$\mathcal{L}(x,y,\textcolor{#0d923f}\lambda)=\textcolor{#0c7f99}{f(x,y)}-\textcolor{#0d923f}\lambda\big(\textcolor{#bc2612}{g(x,y)-c}\big)$$

Để ý rằng, đạo hàm riêng theo $\textcolor{#0d923f}\lambda$ chính bằng điều kiện ràng buộc: $$\mathcal{L}_{\textcolor{#0d923f}\lambda}(x,y,\textcolor{#0d923f}\lambda)=\textcolor{#bc2612}{g(x,y)-c}$$ Đạo hàm theo $x,y$ là: $$ \begin{cases} \mathcal{L}_x(x,y,\textcolor{#0d923f}\lambda)=\textcolor{#0d923f}\lambda\textcolor{#bc2612}{g_x(x,y)} \cr \mathcal{L}_y(x,y,\textcolor{#0d923f}\lambda)=\textcolor{#0d923f}\lambda\textcolor{#bc2612}{g_y(x,y)} \end{cases} $$ Gom lại ta sẽ có: $$\nabla\textcolor{#0c7f99}{f(x,y)}=\textcolor{#0d923f}{\lambda}\nabla\textcolor{#bc2612}{g(x,y)}$$

Như vậy, bài toán của ta sẽ được biến đổi thành dạng tối ưu hàm $\mathcal{L}$ không có điều kiện ràng buộc. Việc này tương đương với giải phương trình gradient của nó bằng véc-to $\mathbf{0}$: $$\nabla\mathcal{L}=\mathbf{0}$$

2.3. Mở rộng

Từ phép biểu diễn như trên ta hoàn toàn có thể tổng quát cho trường hợp có nhiều đẳng thức ràng buộc, khi đó hàm $\mathcal{L}$ được định nghĩa như sau: $$\mathcal{L}(x,y,\textcolor{#0d923f}\lambda)=\textcolor{#0c7f99}{f(x,y)}-\sum_{i=1}^n\textcolor{#0d923f}{\lambda_i}\big(\textcolor{#bc2612}{g_i(x,y)-c_i}\big)$$

Trong đó, $\color{#bc2612}g_i(x,y)=c_i$ là các đẳng thức ràng buộc, còn $\color{#0d923f}\lambda_i$ là các hằng số thành phần tương ứng với mỗi đẳng thức. Việc tối ưu hàm $\color{#0c7f99}f(x,y)$ cũng sẽ được giải gián tiếp qua gradient của $\mathcal{L}$: $$\nabla\mathcal{L}=\mathbf{0}$$

3. Kết luận

Kỹ thuật Lagrange được lấy cảm hứng từ việc tiếp xúc của các đường đồng mức và gradient của chúng. Để tối ưu 1 hàm với ràng buộc là các đẳng thức, ta có thể thực hiện theo kỹ thuật Lagrange như sau:

• Bước 1: Thêm một véc-to nhân tử Lagrange $\color{#0d923f}\lambda$ và định nghĩa một hàm Lagrangian $\mathcal{L}$ như sau: $$\mathcal{L}(\mathbf{x},\textcolor{#0d923f}\lambda)=\textcolor{#0c7f99}{f(\mathbf{x})}-\textcolor{#0d923f}\lambda^{\intercal}\big(\textcolor{#bc2612}{g(\mathbf{x})-c}\big)$$
• Bước 2: Giải đạo hàm (gradient) của $\mathcal{L}$ bằng véc-to $\mathbf{0}$: $$\nabla\mathcal{L}(\mathbf{x},\textcolor{#0d923f}\lambda)=\mathbf{0}$$
• Bước 3: Dựa vào các nghiệm $(\mathbf{x^* },\textcolor{#0d923f}\lambda^* )$ tìm được ở trên, thế vào hàm $\color{#0c7f99}f(\mathbf{x})$ rồi chọn giá trị lớn nhất (nhỏ nhất) là ta được giá trị cần tìm (thực ra chỉ cần nghiệm $\mathbf{x^* }$ là đủ): $$ \begin{cases} \textcolor{blue}{f_{min}} &= \displaystyle\min_{\mathbf{x^* }}\color{#0c7f99}f(\mathbf{x^* }) \cr \textcolor{red}{f_{max}} &= \displaystyle\max_{\mathbf{x^* }}\color{#0c7f99}f(\mathbf{x^* }) \end{cases} $$

Lưu ý rằng do có nhiều đẳng thức ràng buộc nên $\color{#bc2612}g(\mathbf{x})-c$ là một véc-tơ có bậc là số đẳng thức và các nhân tử Lagrange tương ứng cũng là 1 véc-to $\color{#0d923f}\lambda$ có bậc tương đương.