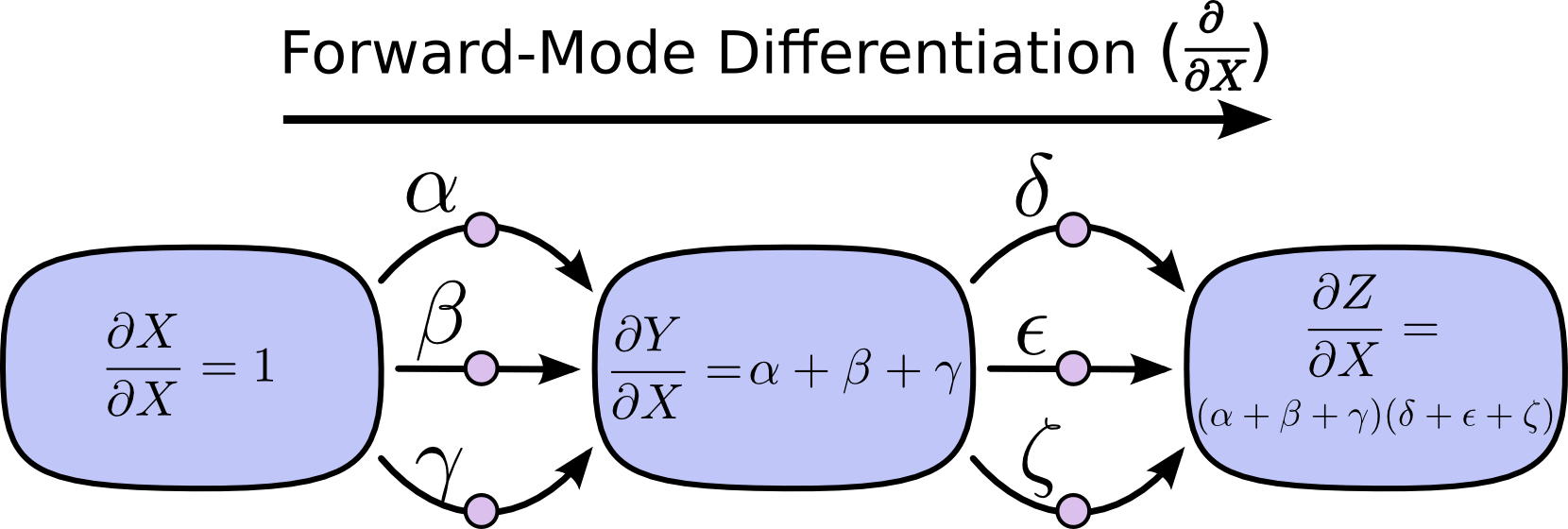[NN] Về lan truyền ngược - Backpropagation
Bài viết này được dịch lại từ bài của anh Christopher Olah bởi anh ấy trình bày rất chi tiết và cực dễ hiểu nên mình không viết lại làm gì cho phí công nữa. Nội dung của bài viết này không phải về chi tiết giải thuật lan truyền ngược mà viết về nguyên lý cơ bản của giải thuật này. Nếu bạn cần xem chi tiết giải thuật được thực hiện ra sao thì có thể đọc bài viết trước của tôi.
Mục lục
1. Giới thiệu
Lan truyền ngược (backpropagation) là giải thuật cốt lõi giúp cho các mô hình học sâu có thể dễ dàng thực thi tính toán được. Với các mạng NN hiện đại, nhờ giải thuật này mà thuật toán tối ưu với đạo hàm (gradient descent) có thể nhanh hơn hàng triệu lần so với cách thực hiện truyền thống. Cứ tưởng tượng 1 mô hình với lan truyền ngược chạy mất 1 tuần thì có thể mất tới 200,000 năm để huấn luyện với phương pháp truyền thống!
Mặc lan truyền ngược được sử dụng cho học sâu, nhưng nó còn là công cụ tính toán mạnh mẽ cho nhiều lĩnh vực khác từ dự báo thời tiết tới phân tích tính ổn định số học, chỉ có điều là nó được sử dụng với những tên khác nhau. Thực ra nó được khai phá lại để sử dụng cho rất nhiều lĩnh vực khác nhau. Nhưng một cách tổng quát không phụ thuộc vào ứng dụng thì tên của nó là “phép vi phân ngược” (reverse-mode differentiation).
Về cơ bản, nó là một kĩ thuật để nhanh chóng tính được đạo hàm. Và nó là một mẹo cần thiết mà bạn cần hành trang cho mình không chỉ trong lĩnh vực học sâu mà còn cho nhiều bài toán tính toán số học khac nữa.
2. Đồ thị tính toán
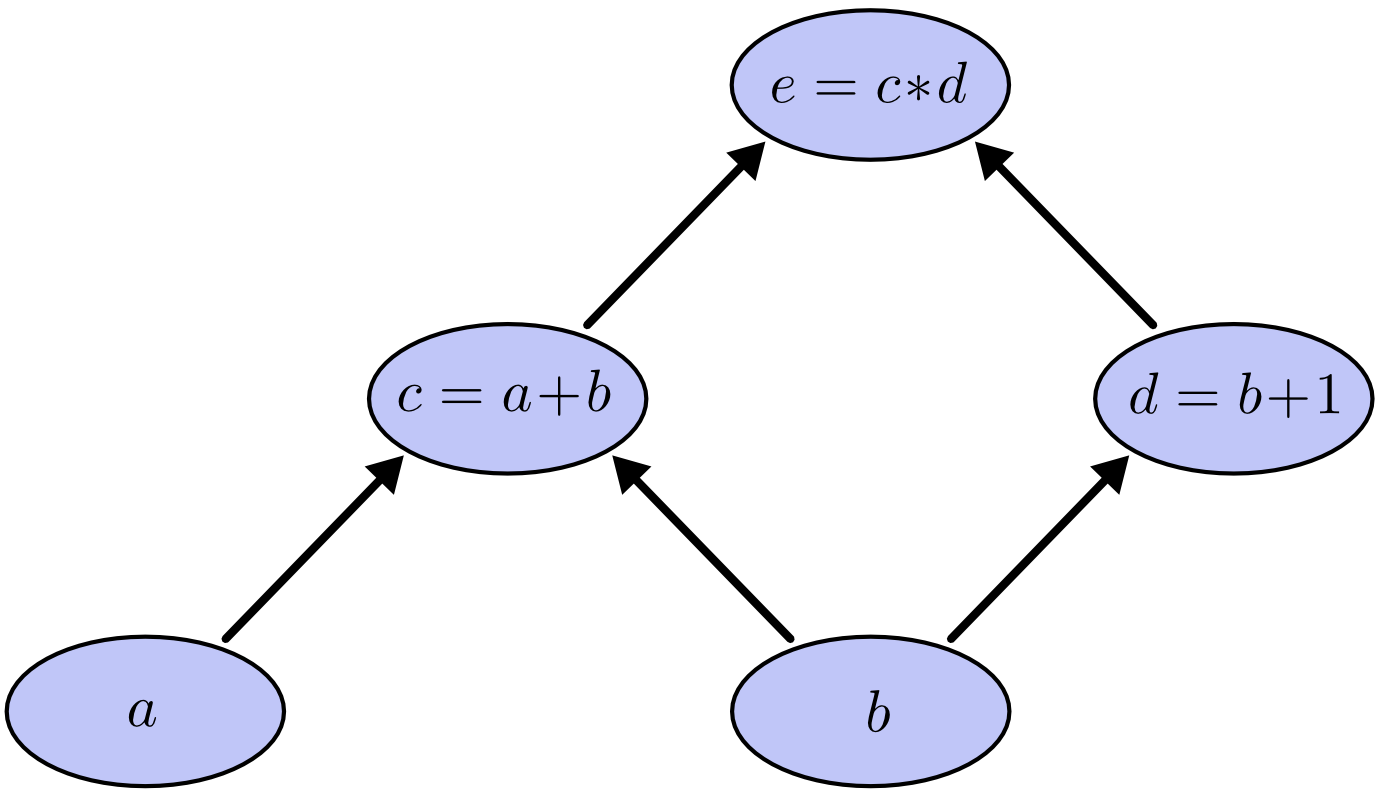
Đồ thị tính toán là một cách hay để hiểu các biểu thức toán học. Ví dụ, với biểu thức $e=(a+b)*b+1)$, ta có 3 phép toán: 2 phép cộng và 1 phép nhận. Để dễ giải thích hơn, ta 2 biến $c, d$ để kết quả mỗi phép tính được gán vào một biến nhất định:
$$ \begin{aligned} c &= a+b \cr d &= b+1 \cr e &= c*d \end{aligned} $$
Để tạo đồ thị tính toán, ta nhóm mỗi phép tính với các biến đầu vào bằng các nút đồ thị. Bằng các mũi tên ta thể hiện đầu ra của một nút là đầu vào cho nút khác.
Computational Graph - Tree defineKiểu đồ thị thế này rất hay được đề cập trong ngành khoa học máy tính, đặc biệt khi nói tới các chương trình hàm. Chúng rất gần với các kí hiệu của đồ thị phụ thuộc và đồ thị gọi. Chúng cũng là ý tưởng chính của các framework phổ biến như Theano chẳng hạn.
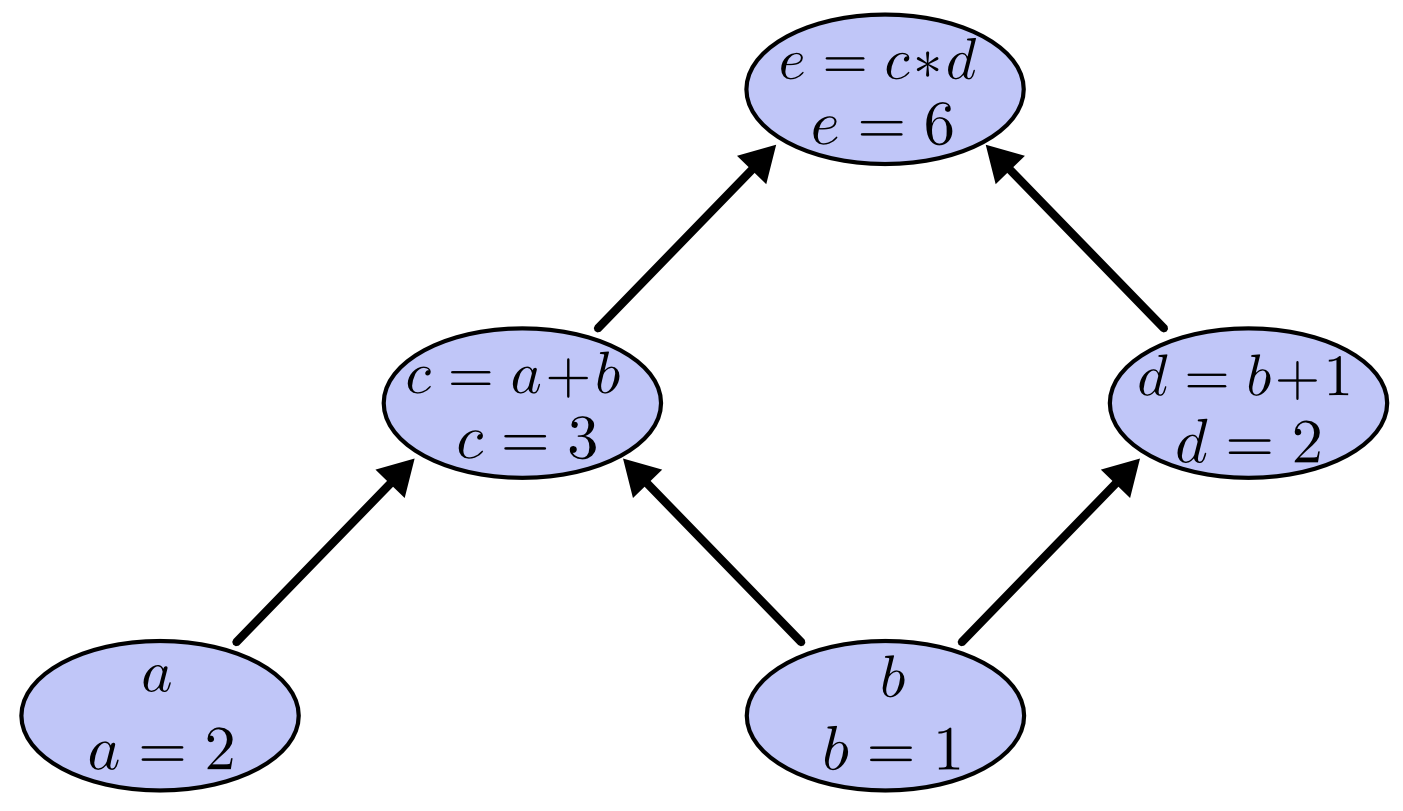
Ta có thể thực hiện các phép toán bằng cách gắn giá trị cho các biến đầu vào bằng các giá trị cụ thể nào đó và tính dần các nút từ dưới lên trên của đồ thị. Ví dụ, gắn $a=2$ và $b=1$, ta được:
Computational Graph - Tree EvalGiá trị thu được là $6$.
3. Đạo hàm với đồ thị tính toán
Nếu muốn hiểu đạo hàm trong đồ thị tính toán, thì chìa khoá là cần hiểu được đạo hàm trên các cạnh của đồ thị. Nếu $a$ ảnh hưởng trực tiếp tới $c$ thì ta muốn biết nó ảnh hưởng tới $c$ thế nào. Nếu $a$ thay đổi một chút thì $c$ sẽ thay đổi ra sao? Ta gọi nó là đạo hàm riêng của $c$ theo $a$.
Để tính các đạo hàm riêng trên đồ thị này, ta cần phải sử dụng luật cộng và luật nhân:
$$ \begin{aligned} & \frac{\partial}{\partial{a}}(a+b)=\frac{\partial{a}}{\partial{a}}+\frac{\partial{b}}{\partial{a}}=1 \cr & \frac{\partial}{\partial{u}}uv=u\frac{\partial{v}}{\partial{u}}+v\frac{\partial{u}}{\partial{u}}=v \end{aligned} $$
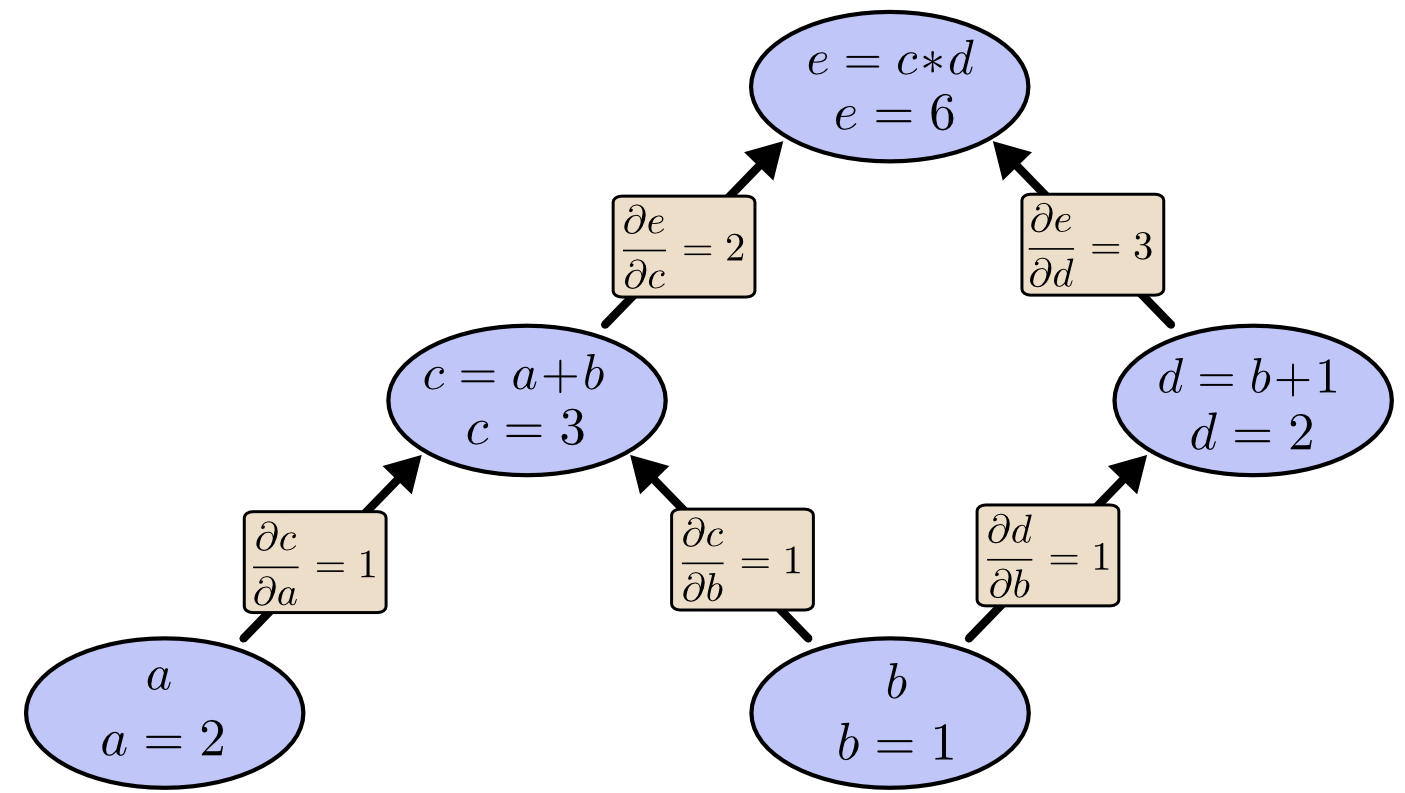
Các đạo hàm trên mỗi cạnh được thể hiện trên đồ thị dưới đây:
Computational Graph - Tree Eval DerivativeNhư vậy, làm sao để biết được một nút bị ảnh hưởng thế nào bởi 1 nút không kết nối trực tiếp? Ví dụ, làm sao để biết $e$ bị ảnh hưởng thế nào bởi $a$. Nếu ta thay đổi $a$ 1 đơn vị, thì $c$ cũng thay đổi 1 đơn vị. $c$ thay đổi 1 đơn vị thì $e$ bị thay đổi 2 đơn vị. Vì vậy, $e$ thay đổi $1*2$ đơn vị theo sự thay đổi của $a$.
Quy tắc chung là lấy tổng tất cả các đường từ một nút tới nút khác và nhân với đạo hàm trên mỗi cạnh tương ứng. Ví dụ, để tính đạo hàm cùa $e$ theo $b$, ta có:
$$ \frac{\partial{e}}{\partial{b}}=1*2+1*3 $$
Điều này có nghĩa rằng $b$ ảnh hưởng thế nào tới $e$ thông qua $c$ (tích: $\dfrac{\partial{e}}{\partial{c}}\dfrac{\partial{c}}{\partial{b}}$) và $d$ (tích: $\dfrac{\partial{e}}{\partial{d}}\dfrac{\partial{d}}{\partial{b}}$).
Quy tắc tổng các đường này chỉ đơn giản là một cách tư duy khác của quy tắc chuỗi đạo hàm đa biến (multivariable chain rule).
4. Thay đổi quy tắc tổng
Vấn đề với luật tổng các đường này là nó rất dễ bị bùng phát tổ hợp nhân theo số cạnh liên kết.
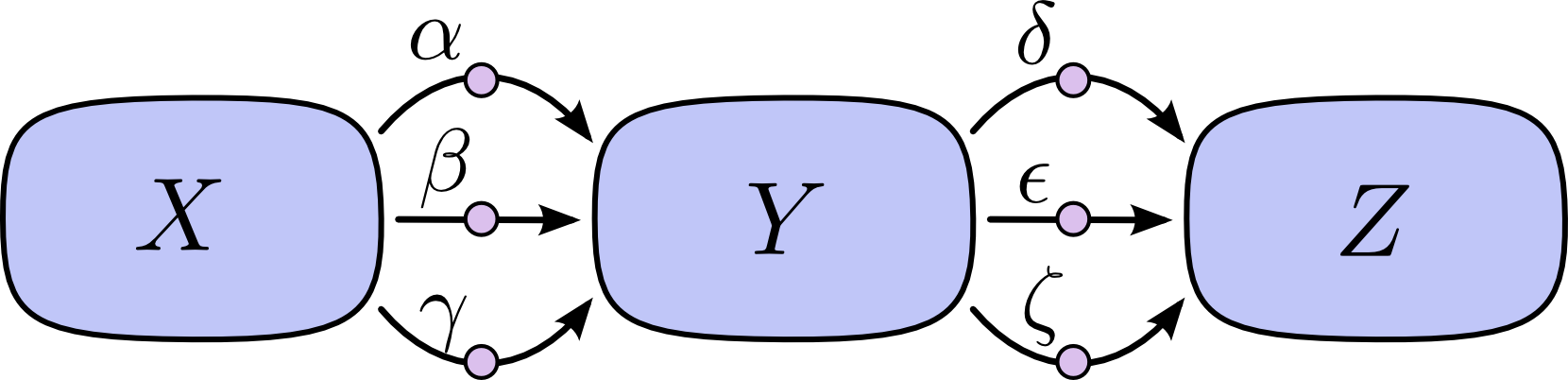
Chain DefineỞ hình trên, ta có 3 cạnh từ $X$ tới $Y$ và có thêm 3 cạnh từ $Y$ tới $Z$. Nếu ta lấy đạo hàm $\dfrac{\partial{Z}}{\partial{X}}$ bằng cách lấy tổng tất cả các đường thì ta sẽ cần phải tính tổng của $3*3=9$ đường tất cả:
$$ \frac{\partial{Z}}{\partial{X}} = \alpha\delta+\alpha\epsilon+\alpha\zeta+\beta\delta+\beta\epsilon+\beta\zeta+\gamma\delta+\gamma\epsilon+\gamma\zeta $$
Ở trên ta chỉ có 8 cạnh, nhưng nó rất dễ bùng nổ số cạnh nếu như đồ thị của ta phức tạp hơn.
Thay vì sử dụng phương pháp truyền thống như vậy, ta có thể biến đổi 1 chút thì nhìn sẽ hiệu quả hơn:
$$ \frac{\partial{Z}}{\partial{X}} =(\alpha+\beta+\gamma)(\delta+\epsilon+\zeta) $$
Đây chính là khởi điểm của 2 phương pháp Đạo hàm tiến (forward-mode differentitation) và Đạo hàm ngược (reverse-mode differentiation). Cả 2 phương pháp là giúp cho việc tính đạo hàm tổng các cạnh trở nên hiệu quả hơn. Thay vì lấy tổng của tất cả các cạnh như truyền thống thì chúng sẽ nhóm các đường cùng tới một nốt với nhau lại rồi tính tổng. Như vậy, mỗi cạnh chỉ cần duyệt 1 lần duy nhất là được!
Đạo hàm tiến bắt đầu từ một nút đầu vào và di chuyển dần tới nút cuối cùng cần tính đạo hàm. Tại mỗi nút, nó sẽ tính tổng tất cả các đường đầu vào của nó. Đương nhiên là mỗi đường như vậy thể hiện một cách ảnh hưởng tới nút tương ứng bởi đầu vào. Bằng cách lấy tổng của chúng, ta sẽ thu được tổng tất cả các cách ảnh hưởng tới nút tương ứng bởi tất cả các đầu vào. Hay nói cách khác, nó chính là đạo hàm của nút tương ứng đó.
Chain ForwardMặc dù có thể bạn không nghĩ cách tính này dựa theo phương pháp đồ thị, nhưng đạo hàm tiến rất gần với cách tính đạo hàm theo mà bạn được học trong các bài giảng về giải tích.
Ngược lại, đạo hàm ngược lại bắt đầu từ đầu ra (điểm cần tính) cho tới đầu vào (điểm bắt đầu). Tại mỗi nút, nó sẽ nhóm tất cả các cạnh xuất phát từ nút tương ứng đó.
Chain BackwardĐạo hàm tiến theo dõi một đầu vào ảnh hưởng tới tất cả các nút ra sao, còn đạo hàm ngược thể hiện tất cả các nút ảnh hưởng tới 1 nút đầu vào thế nào. Nói cách khác, đạo hàm tiến áp dụng phép toán $\dfrac{\partial}{\partial{X}}$ cho tất cả các nút, còn đạo hàm ngược áp dụng phép toán $\dfrac{\partial{Z}}{\partial}$ cho tất cả các nút.
5. Tính toán hiệu quả
Tại thời điểm này, có thể bạn sẽ nghĩ người ta quan tâm tới đạo hàm ngược làm gì khi mà nó có vẻ giống như đạo hàm tiến. Phải chăng nó có những lợi điểm riêng?
Ta cùng xem lại ví dụ trước lần nữa xem sao:
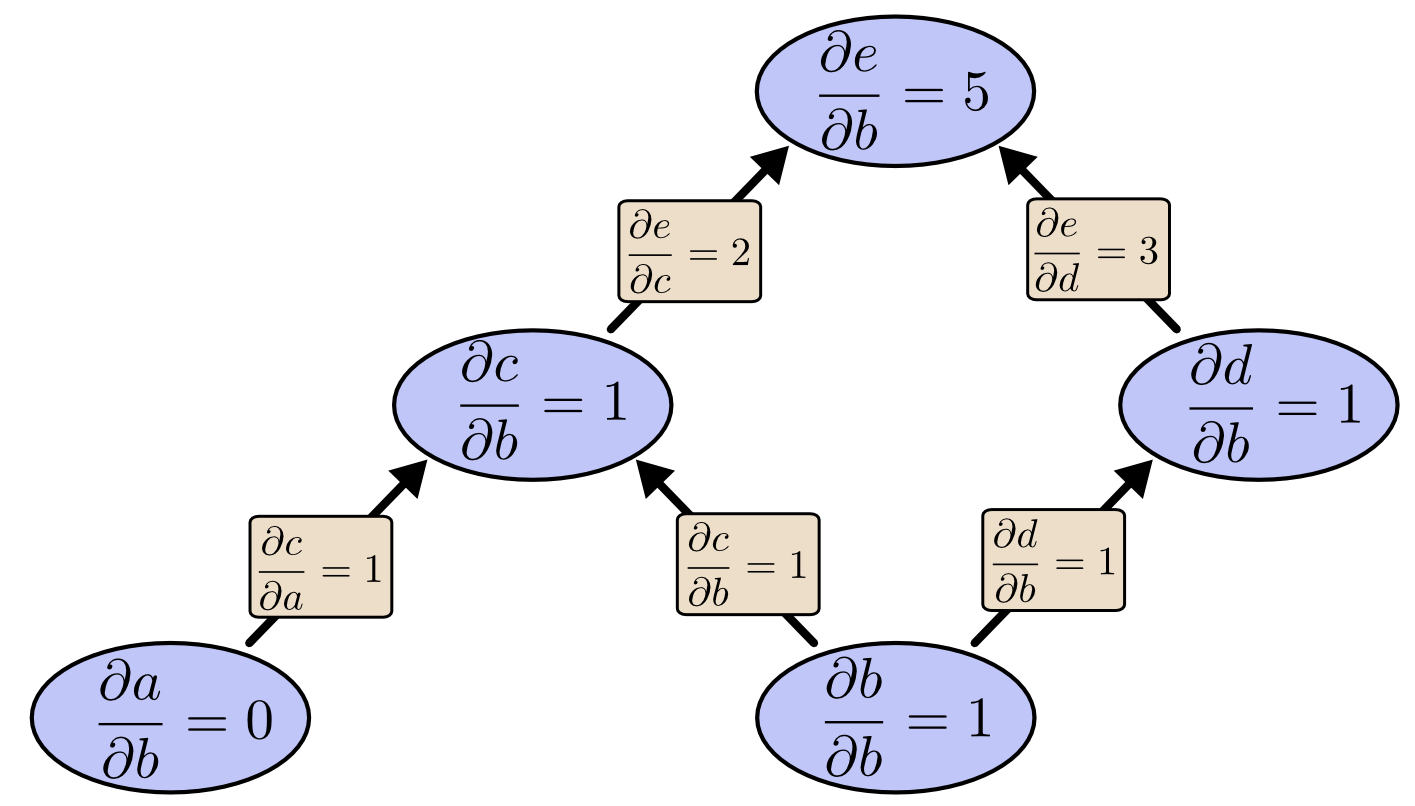
Tree Eval DerivativeTa có thể sử dụng đạo hàm tiến từ $b$ lên trên để thu được đạo hàm của tất cả các nút ảnh hưởng bởi $b$.
Tree Forward ModeTheo cách đó, ta tính được đạo hàm của đầu ra $\dfrac{\partial{e}}{\partial{b}}$ theo một trong các đầu vào.
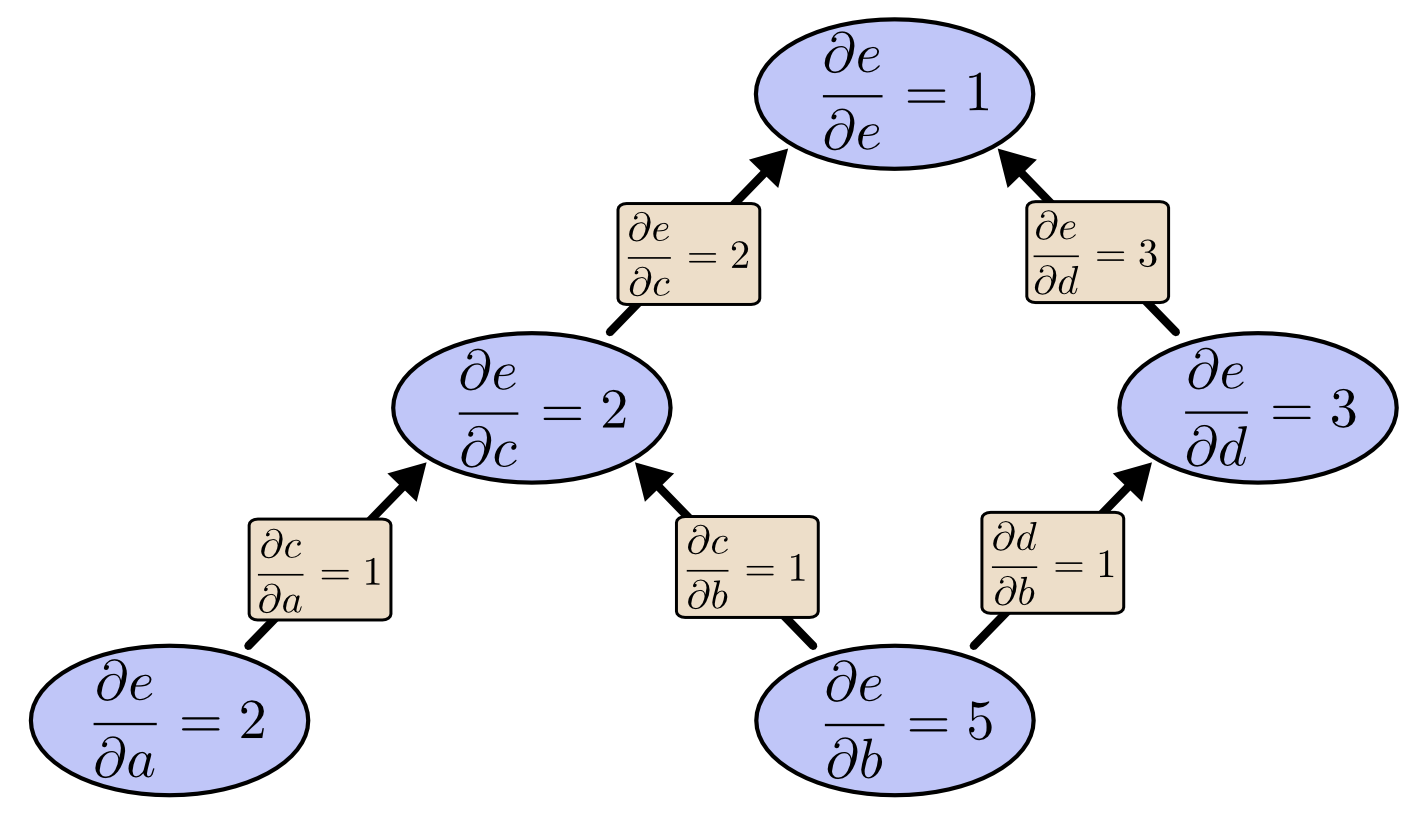
Nhưng nếu ta tính được đạo hàm từ $e$ xuống thì sao? Việc này sẽ cho ta đạo hàm của $e$ theo tất cả các nút:
Tree BackpropKhi tôi nói rằng đạo hàm ngược cho chúng ta đạo hàm của $e$ theo tất cả các nút, tôi thực sự muốn nói rằng tất cả các nút. Ta có thể thu được cả đạo hàm của $e$ theo tất cả các đầu vào $a$ là $\dfrac{\partial{e}}{\partial{a}}$ và $b$ là $\dfrac{\partial{e}}{\partial{b}}$. Đạo hàm tiến cho ta đạo hàm của đầu ra theo một đầu vào, nhưng đạo hàm ngược cho ta tất cả theo đầu vào luôn.
Với đồ thị này, ta thấy rằng tốc độ có lẽ chỉ tăng được đôi chút, nhưng thử tưởng tượng một hàm với 1 triệu đầu vào và 1 đầu ra thì sao. Với đạo hàm tiến ta phải duyệt qua đồ thị 1 triệu lần để có thể tính được đạo hàm. Nhưng với đạo hàm ngược, ta giảm được hẳn xuống còn 1 lần! Tức là tốc đạo nhanh gấp 1 triệu lần! Quá đẹp!
Khi huấn luyện mạng NN, ta quan tâm tới chi phí (một giá trị đánh giá mạng NN của ta tồi tới đâu) như một hàm của các tham số (các số mô tả mạng NN suy diễn thế nào). Khi đó, ta muốn tính đạo hàm của hàm chi phí theo tất cả các tham số để sử dụng cho việc tối ưu hàm chi phí với thuật toán gradient descent. Mà hiện nay, tham số của một mạng NN thường có tới hàng triệu, thậm chí là hàng chục triệu, nên đạo hàm ngược - còn được gọi là lan truyền ngược (backpropagation) trong mạng NN giúp ta tăng tốc lên cực nhiều.
6. Nó có rõ ràng?
Lần đầu tiên khi tôi hiểu lan truyền ngược là gì, thì cảm nhận của tôi là: “Oh, nó chỉ là quy tắc chuỗi thôi mà! Sao mà người ta phải mất nhiều thời gian để tìm ra thế?” Tôi không phải là người duy nhất có cảm nghĩ như vậy. Điều này là đúng nếu bạn hỏi rằng “Có cách nào thông minh để tính đạo hàm trong mạng nơ-ron tiến?” thì câu trả lời không khó tới vậy.
Nhưng tôi nghĩ rằng nó khó hơn ta thấy. Bạn thấy đấy, khi mà lan truyền ngược được sáng tạo, người ta không chú ý lắm tới mạng nơ-ron tiến mà chúng ta tìm hiểu. Cũng không rõ ràng rằng đạo hàm là cách đúng đắn để huấn luyện chúng. Nó chỉ rõ ràng khi bạn nhận ra rằng bạn có thể tính đạo hàm nhanh được. Nó đúng là phụ thuộc vòng.
Xấu nhất thì ta cũng rất dễ dàng vẽ ra các phần của phụ thuộc vòng bằng suy nghĩ thông thường. Huấn luyện mạng NN với các đạo hàm ư? Chắc rằng bạn se chỉ dừng ở các điểm tối ưu cục bộ và rõ ràng chi phí để tính đạo hàm cũng rất tốn kém. Chiến lược này chỉ hoạt động khi ta liệt kê các lý do nó có thể hoạt động.
Đó là lợi ích của kẻ đi sau. Khi bạn đặt ra câu hỏi nào đó thì phần khó nhất được được trả lời trước đó rồi.
7. Kết luận
Đạo hàm ngon hơn là bạn nghĩ. Đó cũng là bài học chính thu được từ bài viết này. Sự thực là nó rất ngon một cách không trực quan và chúng ta phải khám phá lại sự thật đó. Nó là một thứ quan trọng cần phải hiểu trong học sâu. Nó cũng hữu ích trong các lĩnh vực không có cùng kiến thức khác nữa.
Liệu có còn bài học nào khác? Tôi nghĩ là có.
Lan truyền ngược còn là một ống kính hữu ích để hiểu được luồng đạo hàm của một mô hình. Bằng việc vận dụng điều đó ta có thể suy luận được tại sai một vài mô hình lại khó tối ưu. Một ví dụ cơ bản là bài toán mất mát đạo hàm (vanishing gradients) trong mạng nơ-ron hồi quy (RNN - Recurrent neural network).
Cuối cùng, tôi nhận ra một loạt giải thuật lấy ý tưởng từ kĩ thuật này. Lan truyền ngược và đạo hàm tiến được sử dụng như là một cặp mẹo (tuyến tính và quy hoạt động - linearization and dynamic programing) để tính các đạo hảm một cách hiệu quả hơn người ta vẫn nghĩ. Nếu bạn thực sự hiểu những kĩ thuật này, bạn có thể sử dụng chúng hiệu quả để tính các biểu thức thú vị khác có chưa đạo hàm. Ta sẽ cùng khám phá nó trong một bài viết sau.
Bài viết này đưa ra cái nhìn rất tổng quát về hoạt động của lan truyền ngược. Tôi rất khuyến khích bạn đọc bài của Michael Nielsen để có cái nhìn cụ thể và tập trung vào mạng NN tại đây.
Tham khảo thêm:
